E.1.4. Задачи для самостоятельной работы по теме: "Массивы".

Одномерные массивы.
В следующих задачах требуется написать программы, использующие одномерные массивы элементов соответствующего типа.

1. Дана последовательность из 50 чисел. Найти их среднее арифметическое. Найти сколько среди них отличных от последнего числа.

2. Дана последовательность из n вещественных чисел. Вычислить сумму тех элементов последовательности, номера которых совпадают со значениями элементов последовательности.

3. Дана последовательность из n вещественных чисел. Если в результате замены отрицательных элементов последовательности их квадратами элементы будут образовывать неубывающую последовательность, то получить сумму элементов исходной последовательности, в противном случае получить их произведение.

4. Дана последовательность из n вещественных чисел. Преобразовать ее по следующему правилу :
первый элемент равен первому элементу;
второй - max(x1,x2);
третий - max(x1, x2, x3)
. . . . . . . . . . .

5. Дана последовательность из n вещественных чисел. Преобразовать ее по следующему правилу: все отрицательные элементы перенести в ее начало, а все остальные в конец, сохраняя исходное взаимное расположение как среди отрицательных, так и среди остальных элементов.

6. Дана последовательность из n вещественных чисел. Сдвинуть все элементы последовательности циклически на k позиций влево.

7. Дана последовательность изnвещественных чисел. Переменной tприсвоить значениеTrue, если элементы последовательности упорядочены строго по возрастанию.

8. Дана последовательность из n вещественных чисел. Переменной t присвоить значение True, если в последовательности нет нулевых элементов и при этом положительные элементы чередуются с отрицательными.

9. Дана последовательность из n вещественных чисел. Все элементы последовательности с четными номерами, предшествующие первому по порядку элементу с наибольшим значением, домножить на него.

10. Дана последовательность из n вещественных чисел. Поменять в последовательности местами наибольший элемент и элемент с номером m.

11. Дана последовательность из n вещественных чисел. Найти номер первого вхождения данного числа в последовательность или вывести сообщение, что такого числа нет.

12. Дана последовательность из n вещественных чисел. Найти номер последнего вхождения данного числа в последовательность или вывести сообщение, что такого числа нет.

13. Дана последовательность из n натуральных чисел. Переменной t присвоить значение True, если среди элементов последовательности есть хотя бы одно число Фибоначчи.

14. Дана последовательность из n целых чисел. Удалить все элементы последовательности значения которых кратны k.

15. Дана последовательность из n вещественных чисел. Получить последовательность {b₁₀}, где b_i = сумме тех элементов исходной последовательности, которые принадлежат (i-1, i] i=1,10. Если полуинтервал не содержит элементов последовательности, то соответствующее b_i положить равным 0.

16. Дана последовательность из n вещественных чисел. Упорядочить последовательность по убыванию методом пузырька:
последовательно сравниваются пары соседних элементов x_k и x_k+1 (k=1,2,...,n-1) и, если x_k < x_k+1, то они переставляются; тем самым наименьший элемент окажется на своем месте в конце массива; затем этот метод применяется ко всем элементам, кроме последнего, и т.д.

17. Дана последовательность из 99 целых чисел. Получить новую последовательность, выбросив из исходной все элементы со значением max(a1,..., a99).

18. Дана последовательность из n действительных чисел. Получить числа b1,...,bn, где bi - среднее арифметическое всех элементов исходной последовательности, кроме i - того элемента.

19. Даны действительные числа a1,...,a20. Преобразовать эту последовательность по правилу: большее из ai и a10+i (i=1,..., 10) принять в качестве нового значения ai, а меньшее - в качестве нового значения a10+i.

20. Дано натуральное число n. Сколько различных цифр встречается в его десятичной записи.

21. Дана последовательность из 20ти целых чисел. Первый по порядку элемент с наименьшим значением заменить целой частью среднего арифметического всех элементов исходной последовательности, остальные элементы оставить без изменения.

22. Дана последовательность из n действительных чисел. Оставить ее без изменения, если она упорядочена по неубыванию или по невозрастанию; в противном случае получить положительные элементы элементы исходной последовательности упорядоченные по возрастанию.

23. Дана последовательность из n логических значений. Определить, каких значений в последовательности больше - Trueили False.

24. Дана последовательность из 100 логических значений. Если среди них есть хотя бы одно значение False, то вывести False, иначе - True.

Многомерные массивы.
1. Ввести вещественную матрицу размерности n * m построчно, а вывести по столбцам.

2. Выяснить сколько положительных элементов содержит матрица размерности n * m , если a_ij = sin(i+j/2).

3. Дана квадратная вещественная матрица размерности n. Является ли матрица симметричной относительно главной диагонали.

4. Дана квадратная вещественная матрица размерности n. Транспонировать матрицу.

5. Дана квадратная вещественная матрица размерности n. Сравнить сумму элементов матрицы на главной и побочной диагоналях.

6. Дана квадратная вещественная матрица размерности n. Найти количество нулевых элементов, стоящих:
- выше главной диагонали;
- ниже главной диагонали;
- выше и ниже побочной.

7. Сформировать матрицу по следующему правилу
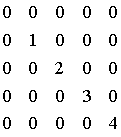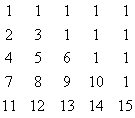а). б). в).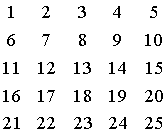

8. Дана вещественная матрица размерности n * m. По матрице получить логический вектор, присвоив его k-ому элементу значение True , если выполнено указанное условие и значение False иначе:
- все элементы k столбца нулевые;
- элементы k строки матрицы упорядочены по убыванию;
- k строка массива симметрична.

9. Дана вещественная матрица размерности n * m. Сформировать вектор b, в котором элементы вычисляются как:
- произведение элементов соответствующих строк;
- среднее арифметическое соответствующих столбцов;
- разность наибольших и наименьших элементов соответствующих строк;
- значения первых отрицательных элементов в столбце.

10. Дана вещественная матрица размерности n * m. Вывести номера столбцов, содержащих только отрицательные элементы.

11. Дана вещественная матрица размерности n * m. Вывести номера строк, содержащих больше положительных элементов, чем отрицательных.

12. Дана вещественная матрица размерности n * m. Найти общую сумму элементов только тех столбцов, которые имеют хотя бы один нулевой элемент.

13. Дана вещественная матрица размерности n * m. Поменять местами строки с максимальным и минимальным элементами.

14. Дана вещественная матрица размерности n * m. Удалить k столбец матрицы.

15. Дана вещественная квадратная матрица размерности n. Поменять местами элементы главной и побочной диагоналей матрицы:
- по строкам;
- по столбцам.

16. Дана вещественная матрица размерности m * n. Упорядочить элементы каждой четной строки по возрастанию.

17. Дана вещественная матрица размерности m * n. Расположить все элементы матрицы по убыванию. Обход матрицы осуществлять по строкам.

18. Дана вещественная матрица размерности m * n. Определить индексы первого нулевого элемента матрицы. Обход матрицы осуществлять по столбцам.

19. Известно положение двух ферзей на шахматной доске. Бьют ли они друг друга?

20. Дана действительная матрица размера n * 9. Найти среднее арифметическое:
а) элементов каждого столбца;
б) элементов каждой строки, имеющей четный номер.

21. Дано натуральное число n. Выяснить, сколько положительных элементов содержит матрица [a_{i j}] ij=1,...,n, если a_{i j}= sin (i+j/2).

22. Дана действительная матрица размера m * n, в которой не все элементы равны 0. Получить новую матрицу путём деления всех элементов данной матрицы на её наибольший по модулю элемент.

23. Дана действительная квадратная матрица порядка n. Вычислить сумму тех из m элементов, расположенных по главной диагонали выше неё, которые превосходят по величине все элементы, расположенные ниже главной диагонали. Если элементов с указанным свойством нет, то вывести соответствующее сообщение.

24. Дана действительная квадратная матрица порядка n. Выяснить, верно ли, что наибольшее из значений элементов главной диагонали больше, чем наименьшее из значений элементов побочной диагонали.

25. Дана действительная матрица размера m? n. Найти сумму наибольшихзначений элементов ее строк.

26. Даны натуральное число n, действительная квадратная матрица порядка n, действительные числа a₁,...,a_n+5. Элементы последовательности a_1,...,a_n+5 домножить на 10, если наибольший элемент матрицы (в предположении, что такой элемент единственный) находится на главной диагонали, и на 0.5 в противном случае.

27. Дана целочисленная квадратная матрица порядка 8. Найти наименьшее из значений элементов столбца, который обладает наибольшей суммой модулей элементов. Если таких столбцов несколько, то взять первый из них.