ЛЕКЦИЯ 5 Теория вероятностей и ее разделы как математический аппарат надежности и технической диагностики
2. Случайные величины. Основные понятия.
3. Случайные величины. Ряд распределения, многоугольник распределения.
2. Математический аппарат теории надежности и технической диагностики Решение любой технической задачи, использующее теоретический подход, включает в себя построение модели, отражающей основные, интересующие исследователя, аспекты функционирования системы и применение соответствующего этой модели математического аппарата.
При решении задач надежности и технической диагностики приходится иметь дело с величинами и системами величии, точное значение которых указать до опыта невозможно. Это случайные величины и функции, характеризующие случайные явления. Изучением случайных явлений занимается теория вероятностей, основные разделы которой, а именно математическая статистика, теория информации, теория массового обслуживания и составляют математический аппарат теории надежности и технической диагностики.
2.1. Математическая статистика Теория вероятностей есть математическая наука, изучающая закономерности в случайных явлениях. (Случайным называют явление, которое при неоднократном воспроизведении одного и того же опыта протекает каждый раз по-иному).
В природе нет ни одного физического явления, в котором не присутствовали бы в той или иной мере элементы случайности. Как бы точно и подробно ни были фиксированы условия опыта, невозможно достигнуть того, чтобы при повторении опыта результаты полностью, и в точности совпали. Попытка одинаково подробно и тщательно проанализировать влияние всех факторов, от которых зависит явление, привела бы к тому, что решение задачи, в силу непомерной громоздкости и сложности, оказалось бы практически не осуществимым и к тому же не имело бы никакой познавательной ценности. Должна существовать принципиальная разница в методах учета основных, решающих, факторов, определяющих в главных чертах течение явления, и вторичных, второстепенных факторов, влияющих на течение явления в качестве "погрешностей" или "возмущений". Элемент неопределенности, сложности, многопричинности, присущий случайным явлениям, требует создания специальных методов для их изучения.
Практика свидетельствует, что при наблюдении совокупности массы однородных, случайных явлений в них обнаруживаются вполне определенные закономерности, своего рода устойчивости, свойственные массовым случайным явлениям. Закономерности, проявляющиеся в этой массе, оказываются практически независимыми от индивидуальных особенностей отдельных случайных явлений, входящих в массу. Эти особенности в массе как бы взаимно погашаются и средний результат массы случайных явлений оказывается практически уже не случайным. Именно эта многократно подтвержденная опытом устойчивость массовых случайных явлений служит базой для применения вероятностных (статистических) методов исследования.
Методы теории вероятностей приспособлены только для исследования массовых случайных явлений. Они не дают возможности предсказать исход отдельного случайного явления, но дают возможность предсказать средний суммарный результат массы однородных случайных явлений, предсказать средний исход массы аналогичных опытов, конкретный исход каждого из которых остается неопределенным, случайным.
Основные понятия и теоремы теории вероятностей были рассмотрены ранее в курсе высшей математики. Здесь же будет изучено применение теории вероятностей к обработке больших совокупностей чисел. Этот раздел теории вероятностей называется математической статистикой. Рассмотрим ее основные положения.
2.1.1. Случайные величины и их законы распределения
а) Основные понятия.
Первым основным понятием является событие. Под событием понимают всякий факт, который в результате опыта может произойти или не произойти. Каждое из событий обладает определенной степенью возможности. Для количественного сопоставления событий по степени их возможности вводится понятие вероятности.
Вероятность события есть численная мера степени объективной возможности, этого события.
Событие, которое в данном опыте не может произойти называется невозможным (его вероятность 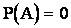 ).
).
Событие, которое в данном опыте обязательно произойдет называется достоверным (его вероятность 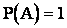 ).
).
Несколько событий в данном опыте образуют полную группу событий , если. в результате опыта обязательно должно появиться хотя бы одно из них.
Несколько событий называются несовместными в данном опыте, если никакие два из них не могут появиться, вместе.
Несколько событий в данном опыте называются равновозможными , если по условиям симметрии есть основание считать, что ни одно из этих событий не является объективно более возможным чем другое.
Если события, образующие полную группу несовместны и равновозможны, то их называют случаями или шансами.
Для случаев подсчет вероятности осуществляется непосредственно:
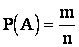 ,
,
где 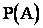 – вероятность события А;
– вероятность события А;
n – общее число случаев;
m – число случаев, благоприятных событию А. (Благоприятным событию называют случай, появление которого влечет за собой появление данного события).
Для событий не являющихся случаями непосредственный подсчет вероятности невозможен. В этой ситуации вероятность события характеризуют его частотой или статистической вероятностью . Частотой события А в данной серии опытов называется отношение числа опытов, в которых появилось событие А, к общему числу произведенных опытов.
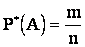 ,
,
где 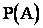 – вероятность события А;
– вероятность события А;
n – число появлений события А;
m –число произведенных опытов.
При возрастании числа опытов n частота приближается к вероятности, но не с полной достоверностью, а с большой вероятностью, которая при достаточно большом числе опытов может рассматриваться как практическая достоверность. Для описания такого характера приближения одних величин к другим введен термин " сходимость по вероятности ".
Противоположными , событиями, называют два несовместных, события, образующих полную группу.
Событие А называется независимым от события В, если вероятность события А не зависит от того, произошло событие В или нет.
Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.
Вероятность события А, вычисленная при условии, что имело место другое событие В, называется условной вероятностью события А и обозначается 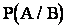 .
.
б) Ряд распределения. Многоугольник распределения.
Важнейшее понятие теории вероятности – случайная величина было введено ранее. Случайной называется величина, принимающая в результате испытания числовое значение, которое принципиально нельзя указать исходя из условий событий. Случайная величина обладает целым набором допустимых значений, но в результате каждого отдельного испытания принимает лишь какое-то одно из них. Чтобы охарактеризовать случайную величину, необходимо задать набор ее допустимых значений. В зависимости от того каков набор, этих значений различают непрерывные и дискретные случайные величины.
Случайная величина называется дискретной , если между. любыми двумя ее значениями заключено лишь конечное число других допустимых значений. Если же возможные значения случайной величины заполняют непрерывно промежуток между любыми двумя ее значениями, то такая случайная величина непрерывная .
Случайные величины будут, обозначаться большими буквами, а их возможные значения – соответствующими малыми.
Рассмотрим дискретную случайную величину X с возможными значениями 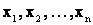 . Каждое из этих значений возможно, но не достоверно и величина X может принять каждые из них с некоторой вероятностью. Обозначим вероятности этих событий буквами р с соответствующими индексами.
. Каждое из этих значений возможно, но не достоверно и величина X может принять каждые из них с некоторой вероятностью. Обозначим вероятности этих событий буквами р с соответствующими индексами.
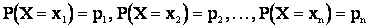
(Так как события 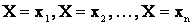 несовместны и образуют полную группу, то
несовместны и образуют полную группу, то 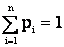 ).
).
Случайная величина X будет полностью описана, с вероятностной точки зрения, если будет указано какой вероятностью обладает каждое из значений 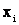 случайной величины X. Этим будет установлен так называемый закон распределения случайней величины.
случайной величины X. Этим будет установлен так называемый закон распределения случайней величины.
Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.
Простейшей формой задания закона распределения дискретной случайной величины является таблица, в которой перечислены возможные значения этой величины и соответствующие им вероятности.
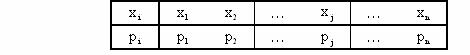
Такую таблицу называют рядом распределения случайной величины.
Графическое представление ряда распределения, имеющее вид рис. 2.1, называют многоугольником распределения .

Рис. 2.1
Дата добавления: 2014-12-03; просмотров: 1288;
