Функциональные и степенные ряды
Рассмотрим ряд
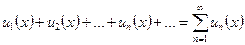 , (7)
, (7)
где все функции  определены в одном и том же промежутке, называемом областью определения ряда. Придавая аргументу
определены в одном и том же промежутке, называемом областью определения ряда. Придавая аргументу 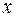 определенные числовые значения, будем получать различные числовые ряды, которые могут оказаться сходящимися или расходящимися.
определенные числовые значения, будем получать различные числовые ряды, которые могут оказаться сходящимися или расходящимися.
Совокупность тех значений х, при которых функциональный ряд сходится, называется областью его сходимости.
В области сходимости сумма функционального ряда является некоторой функцией от х:
 , (8)
, (8)
где 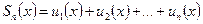 , х принадлежит области сходимости ряда (7).
, х принадлежит области сходимости ряда (7).
Разность
 (9)
(9)
называется n-м остатком ряда.
Так как исследование сходимости функциональных рядов сводится к исследованию сходимости числовых рядов, то для нахождения областей сходимости функциональных рядов можно применять достаточные признаки сходимости числовых рядов. При этом различают области абсолютной и условной сходимости функционального ряда.
Пример. Найти область сходимости степенного ряда
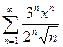 .
.
Решение. Данный степенной ряд можно записать так:
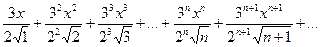 (*)
(*)
Применяем признак Даламбера:
 .
.
Как видно, ряд будет сходиться для тех значений x, для которых
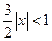 , или
, или 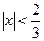 , или
, или  .
.
Выясним вопрос о сходимости ряда на концах интервала.
При 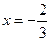 ряд (*) примет вид
ряд (*) примет вид
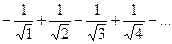 (**)
(**)
Ряд (**) является знакочередующимся; его общий член по абсолютному значению стремится к нулю при  . По признаку Лейбница о сходимости знакочередующихся рядов заключаем, что ряд (**) сходится. Следовательно, значение
. По признаку Лейбница о сходимости знакочередующихся рядов заключаем, что ряд (**) сходится. Следовательно, значение 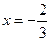 принадлежит области сходимости данного ряда.
принадлежит области сходимости данного ряда.
Подставив в (*) 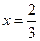 , получим
, получим
 (***)
(***)
Ряд (***) расходится (для этого достаточно сравнить его с гармоническим рядом). Следовательно, значение 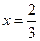 не принадлежит области данного ряда. Таким образом,
не принадлежит области данного ряда. Таким образом, 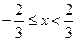 — область сходимости исследуемого ряда.
— область сходимости исследуемого ряда.
Пример.Найти область сходимости функционального ряда 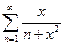 .
.
Решение. Рассмотрим ряд 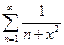 . Сравним его с числовым рядом
. Сравним его с числовым рядом  , используя второй признак сравнения. Найдем предел частного общих членов этих рядов при
, используя второй признак сравнения. Найдем предел частного общих членов этих рядов при  :
:
 .
.
Следовательно, ряд 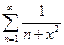 расходится, так как расходится гармонический ряд. Далее воспользуемся теоремой: если ряд
расходится, так как расходится гармонический ряд. Далее воспользуемся теоремой: если ряд 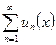 расходится и
расходится и  (с – какое-либо фиксированное число), то ряд
(с – какое-либо фиксированное число), то ряд 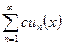 также расходится. В данном случае
также расходится. В данном случае  ,
, 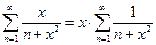 . Значит, при
. Значит, при 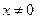 ряд
ряд 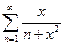 расходится. При
расходится. При 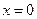 все члены функционального ряда
все члены функционального ряда 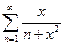 равны нулю,
равны нулю, 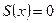 при
при 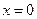 , т.е. ряд сходится. Итак, данный ряд расходится при всех х, кроме
, т.е. ряд сходится. Итак, данный ряд расходится при всех х, кроме 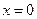 .
.
Пример.Найти область сходимости функционального ряда
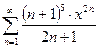 .
.
Решение. Воспользуемся признаком Даламбера:
 ,
, 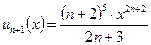 ;
;
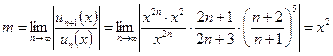 .
.
При m < 1 данный ряд будет сходиться, т.е. x2 < 1, |x| < 1, –1 < x < 1.
Исследуем границы интервала 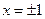 . При
. При 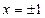 получим ряд
получим ряд 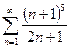 , который расходится, так как
, который расходится, так как 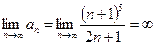 . Следовательно, областью сходимости данного ряда является интервал
. Следовательно, областью сходимости данного ряда является интервал 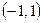 .
.
Дата добавления: 2014-12-05; просмотров: 1703;
