Равномерная сходимость функционального ряда

Для каждого значения x₀ из области сходимости ряда 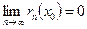, т.е. остаток 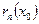сходящегося ряда стремится к нулю при .

Определение. Функциональный ряд 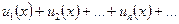называется равномерно сходящимся в некотором интервале, если он сходится для всех x из этого интервала и если для всякого числа e>0 существует такое число N>0, зависящее от e и не зависящее от x. (при n > N выполняется неравенство 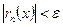для всех x из рассматриваемого интервала).

Для установления равномерной сходимости функционального ряда на отрезке служат и достаточные признаки равномерной сходимости. Один из них признак Вейерштрасса.

Теорема (признак Вейерштрасса)

Если существует сходящийся числовой ряд с положительными членами 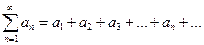и при этом выполняются соотношения: 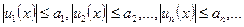для всех 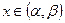, в котором определены члены функционального ряда 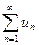, то этот ряд сходится равномерно (и абсолютно) в интервале .

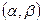В этом случае ряд 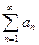, члены которого превосходят абсолютные величины соответствующих членов ряда 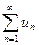, называется мажорантным рядом для .

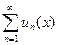Примечание. Если сходится ряд 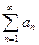, то можно найти такое положительное целое число 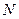(номер), не зависящее от 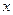, что при 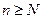модуль 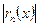будет меньше любого наперед заданного положительного числа .

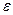Вопросы для самопроверки

1. Дайте определение сходимости функционального ряда. Приведите примеры рядов с различными областями сходимости.
2. Дайте определение понятия равномерной сходимости последовательной функции. Какой ряд называется равномерно сходящимся?
3. Сформулируйте признак абсолютной и равномерной сходимости ряда.
4. Сформулируйте основные свойства равномерно сходящихся рядов.
5. Докажите теорему Абеля о сходимости степенных рядов.
6. Выведите формулу для вычисления радиуса круга сходимости степенного ряда.