Классическое определение вероятности. Классическое определение вероятности события формулируют следующим образом:

Классическое определение вероятности события формулируют следующим образом:

Вероятность Р(А) события А равна отношению числа возможных результатов опыта m, благоприятствующих событию А, к числу всех возможных результатов опыта n:

.

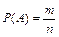Пример.Подбрасывание игральной кости один раз. Событие А состоит в том, что выпавшее число очков - четно. В этом случае n= 6 -число граней куба; m= 3 - число граней с четными номерами; тогда .

Вычисление вероятности по формуле 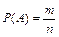вызывает в некоторых случаях затруднения при определении значений m и n. Эти затруднения связаны, в частности, с тем, что при решении ряда задач требуется применение формул из комбинаторики. Поэтому полезными являются нижеследующиекомбинаторные формулы.

Число всевозможных перестановок из n различных элементов равно n! (читается "эн факториал" и обозначает произведение всех целых чисел от 1 до n, т.е. n!=1·2·З...n, по определению 0! =1).

Например, число способов рассадить 4-х человек на 4-х местах равно 4! = 1·2·3·4 =24.

Число всевозможных способов выбрать m элементов из n элементов (порядок, в котором выбирались элементы, роли не играет) называют числом сочетаний из n по m, обозначают .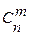

Справедлива формула .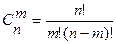

Например, число способов выбрать трех дежурных из группы в 20 человек равно .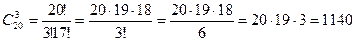

Число всевозможных способов выбрать m элементов из n в определенном порядке называют числом размещений из n элементов по m, обозначают .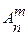

Справедлива формула .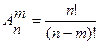

Например, число способов выбрать председателя и секретаря собрания, если в нем участвуют 20 человек, равно .

Пример. Набирая номер телефона, абонент забыл две последние цифры. Какова вероятность того, что он с первого раза наберет эти цифры правильно, если он помнит, что они различны?

Решение. Обозначим А - событие, состоящее в том, что абонент, набрав произвольно две цифры, угадал их правильно. m - число правильных вариантов, очевидно, что m= 1; n - число различных цифр, .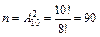

Таким образом, .