Произведение событий. Условная вероятность. Теоремы умножения вероятностей.
Событие, состоящее в наступлении обоих событий А и В, называют произведением (или пересечением)событий А и Ви обозначают А·В.
Понятие условной вероятности является основным инструментом теории вероятностей.
Вероятность события А в предположении, что уже произошло событие В, называютусловной вероятностью события А при условии В и обозначают Р(А|В)
Вероятность произведения двух событий равна произведению вероятности одного из событий на условную вероятность другого при условии, что первое произошло:
Р(А·В)=Р(А)·Р(В/А)=Р(В)·Р(А|В).
Из теоремы умножения следует формула для вычисления условной вероятности события Р(А|В)= 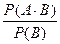 .
.
События А и В называютнезависимыми, если вероятность произведения событий равна произведению соответствующих вероятностей Р(А·В)=Р(А)·Р(В).
Если события А и В независимы, то условная вероятность равна Р(А|В)безусловнойР(А), а условная вероятность Р(В|А) равна безусловной вероятности Р(В).
Пример. Студент пришел сдавать зачет, зная из 30 вопросов только 20. Какова вероятность сдать зачет, если после отказа отвечать на первый вопрос, преподаватель задает еще один?
Решение. Обозначим события:
А - студент сдал зачет;
В - студент ответил на первый вопрос преподавателя;
С - студент ответил на второй вопрос преподавателя.
Ясно, что 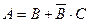 - т.е. студент сдаст зачет, если либо он ответит на первый вопрос, либо не ответит на первый, но ответит на второй.
- т.е. студент сдаст зачет, если либо он ответит на первый вопрос, либо не ответит на первый, но ответит на второй.
По теореме сложения
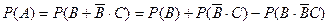 ,
,
По условию задачи 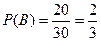 .
.
По теореме умножения Р( 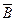 ·С)=Р(С|
·С)=Р(С| 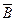 )·Р(
)·Р( 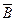 ).
).
Р(В)=0,6+0,1-0,4 =0,3.
Далее, Р( 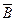 )=1–Р(В)=
)=1–Р(В)= 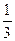 ;
;
Р(С| 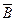 ) - вероятность ответить на второй вопрос при условии, что студент не ответил на первый.
) - вероятность ответить на второй вопрос при условии, что студент не ответил на первый.
Р(С| 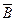 )=
)= 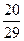 , так как осталось 29 вопросов, из них студент знает 20.
, так как осталось 29 вопросов, из них студент знает 20.
Таким образом, 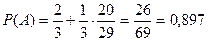 .
.
Дата добавления: 2014-12-05; просмотров: 1469;
