Локальная и интегральная теоремы Лапласа
При достаточно большом 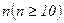 формула Бернулли дает громоздкие вычисления. Поэтому в таких случаях применяют локальную теорему Лапласа.
формула Бернулли дает громоздкие вычисления. Поэтому в таких случаях применяют локальную теорему Лапласа.
Теорема(локальная теорема Лапласа). Если вероятность pпоявления события А в каждом испытании постоянна и отлична от 0 и 1, то вероятность 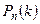 того, что событие А появится в n независимых испытаниях ровно k раз, приближенно равна значению функции:
того, что событие А появится в n независимых испытаниях ровно k раз, приближенно равна значению функции:
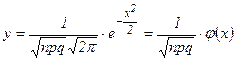 ,
,
где
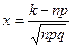 .
.
Имеются таблицы, в которых находятся значения функции 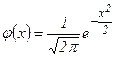 , для положительных значений x.
, для положительных значений x.
Заметим, что функция 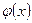 четна.
четна.
Итак, вероятность того, что событие А появится в n испытаниях ровно k раз приближенно равна
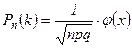 , где
, где 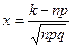 .
.
Пример.На опытном поле посеяли 1500 семян. Найти вероятность того, что всходы дадут 1200 семян, если вероятность того, что зерно взойдет, равна 0,9.
Решение. 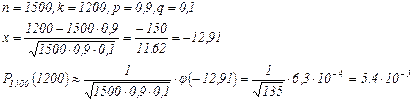
Дата добавления: 2014-12-05; просмотров: 1369;
