Интегральная теорема Лапласа

Вероятность того, что в n независимых испытаниях событие А появится не менее k1 раз и не более k2 раз вычисляется по интегральной теореме Лапласа.

Теорема(интегральная теорема Лапласа). Если вероятность р наступления события а в каждом испытании постоянна и отлична от 0 и 1, то вероятность того, что событие А в n испытаниях появится не менее k₁раз и не более k₂ раз приближенно равна значению определенного интеграла:

,

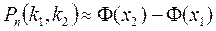где

.

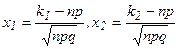Функция 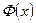называется интегральной функцией Лапласа, она нечетна и ее значение находятся по таблице для положительных значений x.

Пример. В лаборатории из партии семян, имеющих всхожесть 90%, высеяно 600 семян, давших всходы, не менее 520 и не более 570.