Інтегральна теорема

Обчислення ймовірностей за формулою Бернуллі при великих значеннях n і m пов’язане з певними труднощами. Щоб уникнути їх, застосовують асимптотичні формули, що випливають з інтегральної теорем Муавра—Лапласа.

Якщо ймовірність появи випадкової події в кожному з n незалеж­них експериментів є величиною сталою і дорівнює 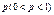, то для великих значень n імовірність появи випадкової події від m_і до m_j раз обчислюється за такою асимптотичною формулою:

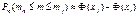, (45)

де ,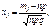

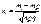а 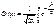є функцією Лапласа, значення якої наведено в додатках

Доведення. Імовірність того, що в результаті n незалежних експериментів подія відбудеться від m_і до m_j раз, обчислюється за формулою .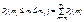

Згідно з (35) для досить великого числа спроб n маємо наближену рівність: ,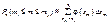

де ; .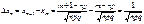

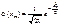Отже, можна записати: .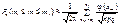

Тут (46) є інтегральною сумою, а тому

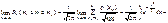
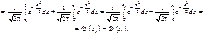
Для великих, але обмежених значень n дістанемо:

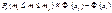, що й потрібно було довести.