Локальна теорема
Обчислення ймовірностей за формулою Бернуллі при великих значеннях n і m пов’язане з певними труднощами. Щоб уникнути їх, застосовують асимптотичні формули, що випливають з локальної теорем Муавра—Лапласа.
Якщо ймовірність появи випадкової події в кожному з n незалежних експериментів є величиною сталою і дорівнює 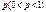 , то для великих значень n і m імовірність того, що випадкова подія А настане m раз, подається такою асимптотичною формулою:
, то для великих значень n і m імовірність того, що випадкова подія А настане m раз, подається такою асимптотичною формулою:
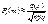 , (35)
, (35)
де 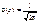 ℮
℮ 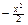 називається функцією Гаусса. Функція Гаусса протабульована, і її значення наведено в дод. 1, де
називається функцією Гаусса. Функція Гаусса протабульована, і її значення наведено в дод. 1, де
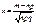 . (36)
. (36)
Тут x є рівномірно обмеженою величиною відносно n і m.
Коли n ® ∞, маємо:
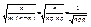 .
.
Розклавши логарифмічні функції у ряд Тейлора і обмежившись двома членами ряду,
При  маємо:
маємо:
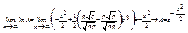
Отже,
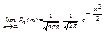 ,
,
а для великих, хоча й обмежених значень n
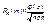 ,
,
що й потрібно було довести.
Властивості функції Гаусса:
1) 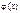 визначена на всій осі абсцис;
визначена на всій осі абсцис; 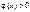 ;
;
2) 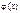 є функцією парною:
є функцією парною: 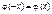 ;
;
3) 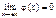 ;
;
4) 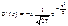 ;
; 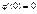 ;
;
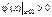 ;
; 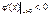 ; отже,
; отже, 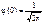 — максимум функції Гаусса;
— максимум функції Гаусса;
5) 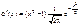
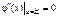 .
.
Таким чином, х1 = –1, х2 = 1 будуть точками перегину. При цьому
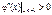 ;
; 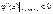 ;
; 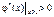 .
.
Графік функції Гаусса зображено
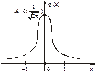 Рис. 15
Рис. 15
Зауважимо, що розв’язуючи задачі, додержують такого правила:
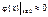 ;
; 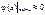 .
.
Приклад 1. Фабрика випускає 75% виробів 1-го сорту. Із партії готових виробів навмання беруть 400 деталей. Обчислити ймовірності таких випадкових подій:
1) виробів 1-го сорту виявиться 290 шт.;
2) 300 шт.;
3) 320 шт.

 Розв’язання. За умовою задачі маємо:
Розв’язання. За умовою задачі маємо:
n = 400; p = 0,75; q = 0,25; m = 290; 300; 320.
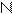 1)
1) 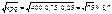 ;
; 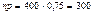 ;
;
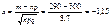 ;
;
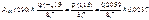 ;
;
2) 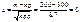 ;
;
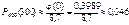 ;
;
3) 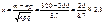 ;
;
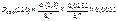 .
.
Дата добавления: 2014-11-29; просмотров: 1443;
