Використання інтегральної теореми
За допомогою 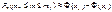 , можна оцінити близькість відносної частоти W(А) до ймовірності p випадкової події А. Нехай p — імовірність появи випадкової події А в кожному експерименті за схемою Бернуллі й W(А) — відносна частота появи цієї події при n експериментах.
, можна оцінити близькість відносної частоти W(А) до ймовірності p випадкової події А. Нехай p — імовірність появи випадкової події А в кожному експерименті за схемою Бернуллі й W(А) — відносна частота появи цієї події при n експериментах.
Необхідно оцінити ймовірність події ôW(A) – рô< e (e > 0 і є малою величиною). Якщо n набуває великих значень, то можна за формулою 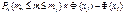 , дістати:
, дістати:
Р(|W(A) – p| < e) 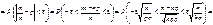
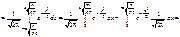
= 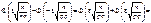
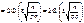 .
.
Отже,
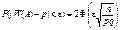 . (46а)
. (46а)
Приклад 1. Імовірність виходу з ладу виробу під час проведення експерименту, який має на меті виявити надійність виробу в роботі, дорівнює 0,2. Було перевірено 400 виробів. Чому дорівнює ймовірність такої події: абсолютна величина відхилення відносної частоти виходу із ладу виробів від імовірності p = 0,2 становить e = 0,01?
Розв’язання. За умовою задачі: n = 400; p = 0,2; q = 0,8; e = 0,01. Підставивши ці значення в (46), дістанемо:
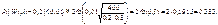
Дата добавления: 2014-11-29; просмотров: 1146;
