Формула Пуассона для малоймовірних випадкових подій
Точність асимптотичних формул для великих значень n — числа повторних незалежних експериментів за схемою Бернуллі — знижується з наближенням p до нуля. Тому при 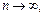
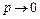 за умови np = a =const імовірність появи випадкової події m раз
за умови np = a =const імовірність появи випадкової події m раз 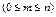 обчислюється за такою асимптотичною формулою:
обчислюється за такою асимптотичною формулою:
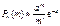 , (47)
, (47)
яка називається формулою Пуассона.
| ! |
Доведення. Оскільки а = np, то 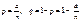 .
.
Запишемо формулу Бернуллі у такому вигляді:
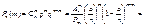
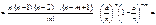
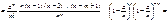
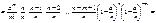
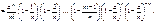
Коли 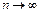 , дістаємо:
, дістаємо:
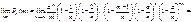
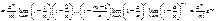 .
.
Оскільки 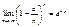 ,
,
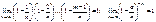 .
.
Отже,
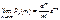 ,
,
а для великих, але обмежених значень n маємо:
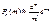 , що й потрібно було довести.
, що й потрібно було довести.
Із (47) випливає:
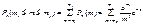 ; (48)
; (48)
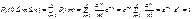 .
.
І справді, це підтверджується ще й тим, що події 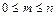 утворюють повну групу.
утворюють повну групу.
Функція Рn (m) визначається за таблицею, наведеною в дод. 3, за заданим m і обчисленим значенням а = np.
Приклад 1. Радіоприлад містить 1000 мікроелементів, які працюють незалежно один від одного, причому кожний може вийти з ладу під час роботи приладу з імовірністю р =
= 0,002. Обчислити ймовірності таких випадкових подій:
1) під час роботи приладу з ладу вийдуть 3 мікроелементи; 2) від трьох до шести.
Розв’язання. За умовою задачі маємо n = 1000; p = 0,002; m = 3; 3 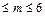 . Оскільки n велике, а р мале число, то для обчислення ймовірностей застосуємо формули (47) і (48). Для цього обчислимо значення параметра а = np = 1000 · 0,002 = 2.
. Оскільки n велике, а р мале число, то для обчислення ймовірностей застосуємо формули (47) і (48). Для цього обчислимо значення параметра а = np = 1000 · 0,002 = 2.
1) 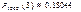 .
.
2) 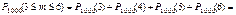
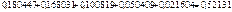
Дата добавления: 2014-11-29; просмотров: 1911;
