Функція розподілу ймовірностей (інтегральна функція) та її властивості

Закон розподілу ймовірностей можна подати ще в одній формі, яка придатна і для дискретних, і для неперервних випадкових величин, а саме: як функцію розподілу ймовірностей випадкової величини F(х), так звану інтегральну функцію.

Функцію аргументу х, що визначає ймовірність випадкової події Х < x, називають функцією розподілу ймовірностей:

F(x) = P(X < x) (62)

Цю функцію можна тлумачити так: унаслідок експерименту випадкова величина може набути значення, меншого за х .

Розглянемо властивості F(x):

1.

Ця властивість випливає з означення функції розподілу.

2. є неспадною функцією, а саме , якщо .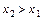

Доведення.Позначимо відповідно А, В, С події (Х < x₂), (Х < x₁) і 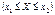. Випадкові події В і С є несумісними (А 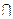С = Æ) / Тоді подію А можна записати так:

А = В 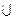С (А = В + С).

За формулою додавання для несумісних випадкових подій (6) маємо:

Р(А) = Р(В С) = Р(В) + Р(С)

або

Р(Х < x₂) = Р(Х < x₁) + P(x₁ £ Х £ х₂). (63)

Звідси на підставі означення інтегральної функції F(x), дістаємо

F(x₂) = F(x₁) + P(x₁ £ Х £ х₂)

або

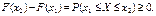(64)

Отже,

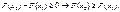
Із другої властивості F(x) випливають наведені далі висновки:

1. Імовірність того, що випадкова величина Х набуде можливого значення 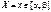, дорівнює приросту інтегральної функції F(x) на цьому проміжку:

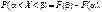(65)

2. Якщо випадкова величина Х є неперервною, то ймовірність того, що вона набуде конкретного можливого значення, завжди дорівнює нулю:

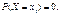
І справді, поклавши в (65) 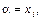, дістанемо

.

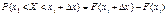Коли 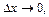маємо:

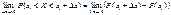. (66)

Оскільки при 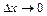Х = х_і, то

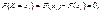
що й потрібно було довести.

Отже, для неперервної випадкової величини Х справджуються такі рівності:

(67)

3. Якщо , виконуються два подані далі співвідношення.

1)

Оскільки подія Х < – ¥ полягає в тому, що випадкова величина набуває значення, яке міститься ліворуч від – ¥. А така подія є неможливою (Æ).

2)

Подія Х < полягає в тому, що випадкова величина Х набуває числового значення, яке міститься ліворуч від + ¥. Ця подія є віро-
гідною (Ώ), оскільки будь-яке число X = x < .

Із цих двох співвідношень випливає висновок: якщо можливі значення випадкової величини Х належать обмеженому проміжку [а; b], то

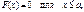
(68)

Приклад 6.Закон розподілу дискретної випадкової величини Х задано таблицею:

Побудувати F(x) та її графік.

Розв’язання. Згідно з властивостями F(x), дістаємо наведені далі співвідношення.

1) F(– 4) = P(X < – 4) = 0;

2) F(–1) = P(X < –1) = P(X = – 4) = 0,1;

3) F(2) = P(X < 2) = P(X = – 4) + P(X = –1) = 0,1 + 0,2 = 0,3;

4)F(6) = P(X < 6) = P(X = – 4) + P(X = –1) + P(X = 2) = 0,1 + 0,2 +
+ 0,1 = 0,4;

5) F(9) = P(X < 9) = P(X = – 4) + P(X = –1) + P(X = 2) + P(X = 6) =
= 0,1 + 0,2 + 0,1 + 0,3 = 0,7;

6) F(12) = P(X < 13) = P(X = – 4) + P(X = –1) + P(X = 2) + P(X = 9) =
= 0,1 + 0,2 +0,1 + 0,3 + 0,1 = 0,8;

7) F(x)|_{x >13} = P(X > 13) = P(X = – 4) + P(X = –1) + P(X = 2) + P(X = 9) +
+ P(X = 13) = 0,1 + 0,2 +0,1 + 0,1 + 0,3 + 0,1 + 0,2 = 1.

Компактно F(x) можна записати в такій формі: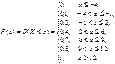

Графік функції F(x) зображено на рис. 23.

Рис. 23