Дискретні та неперервні випадкові величини. Закони розподілу їх імовірностей
Розглянемо такий простір елементарних подій, в якому кожній елементарній події 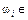 Ώ відповідає одне і лише одне число х або набір чисел
Ώ відповідає одне і лише одне число х або набір чисел 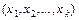 , тобто на множині Ώ визначена певна функція
, тобто на множині Ώ визначена певна функція 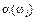 , яка кожній елементарній події
, яка кожній елементарній події  ставить у відповідність певний елемент одновимірного простору R1 або n-вимірного простору Rn.
ставить у відповідність певний елемент одновимірного простору R1 або n-вимірного простору Rn.
Цю функцію називають випадковою величиною. У разі, коли 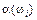 відображає множину Ώ на одновимірний простір R1, випадкову величину називають одновимірною. Якщо відображення здійснюється на Rn, то випадкову величину називають n-вимірною (системою n випадкових величин або n-вимірним випадковим вектором).
відображає множину Ώ на одновимірний простір R1, випадкову величину називають одновимірною. Якщо відображення здійснюється на Rn, то випадкову величину називають n-вимірною (системою n випадкових величин або n-вимірним випадковим вектором).
Схематично одновимірну випадкову величину унаочнює рис. 19.
 Рис. 19
Рис. 19
Отже, величина називається випадковою, якщо внаслідок проведення експерименту під впливом випадкових факторів вона набуває того чи іншого можливого числового значення з певною ймовірністю.
Якщо множина можливих значень випадкової величини є зчисленною то таку величину називають дискретною. У противному разі її називають неперервною.
Приклад 1. Задано множину цілих чисел Ώ = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}. Навмання беруть одне число. Елементарними подіями будуть такі: поява одного з чисел 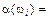 1, 2, 3, …,10 з певною ймовірністю. Множина можливих значень
1, 2, 3, …,10 з певною ймовірністю. Множина можливих значень 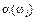 є дискретною, а тому й випадкова величина — поява одного з чисел множини Ώ — буде дискретною.
є дискретною, а тому й випадкова величина — поява одного з чисел множини Ώ — буде дискретною.
Випадкові величини позначають великими літерами латинського алфавіту X, Y, Z, ... , а їх можливі значення — малими х; у; z, ... .
Для опису випадкової величини необхідно навести не лише множину можливих її значень, а й указати, з якими ймовірностями ця величина набуває того чи іншого можливого значення.
З цією метою вводять поняття закону розподілу ймовірностей.
Співвідношення, що встановляє зв’язок між можливими значеннями випадкової величини та відповідними їм імовірностями, називають законом розподілу випадкової величини.
Закон розподілу дискретної випадкової величини Х можна задати в табличній формі або за допомогою ймовірнісного многокутника.
У разі табличної форми запису закону подається послідовність можливих значень випадкової величини Х, розміщених у порядку зростання, та відповідних їм імовірностей:
| Х = хі | х1 | х2 | х3 | ...... | хk |
| Р(Х = хі) = рі | р1 | р2 | р3 | ..... | рk |
Оскільки випадкові події (Х = хj) і (Х = хm) є між собою несумісними ((Х = хі) ∩ (Х = хm) = Æ, і 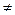 m; і, m = 1, 2, …, k) і утворюють повну групу
m; і, m = 1, 2, …, k) і утворюють повну групу 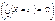 , то необхідною є така умова:
, то необхідною є така умова:
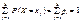 (61)
(61)
Рівність (61) називають умовою нормування для дискретної випадкової величини Х. Наведену таблицю називають рядом розподілу.
| Х = хі | –4 | ||||
| Р(Х = хі) = рі | 0,1 | 0,1 | 0,5 | р4 | 0,2 |
Приклад 3. Закон розподілу дискретної випадкової величини Х задано таблицею
Знайти ймовірність можливого значення випадкової величини Х = х4 = 5.Розв’язання. Згідно з умовою нормування (61) маємо:
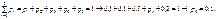
Дата добавления: 2014-11-29; просмотров: 1890;
