Щільність імовірностей (диференціальна функція) f (x) і її властивості

Для неперервних випадкових величин закон розподілу ймовір-
ностей зручно описувати з допомогою щільності ймовірностей, яку позначають f (x).

Щільністю ймовірностей неперервної випадкової величини Х називається перша похідна від інтегральної функції F(x):

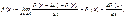(69)

звідки

Оскільки

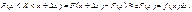
то добуток f (x) dx — ймовірність того, що випадкова величина Х міститиметься у проміжку [х, х + dx], де .

Геометрично на графіку щільності ймовірності f (x) dx відповідає площа прямокутника з основою dx і висотою f (x) (рис. 27а).

Рис. 27а

Властивості f (x)

1. . Ця властивість випливає з означення щільності ймовірності як першої похідної від F(x) за умови, що F(x) є неспадною функцією.

2. Умова нормування неперервної випадкової величини Х:

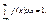(70)

Доведення.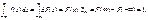

Якщо неперервна випадкова величина Х визначена лише на проміжку [a; b], то умова нормування має такий вигляд: (71)

3. Імовірність попадання неперервної випадкової величини в інтервалі обчислюється за формулою

(72)

Доведення. За властивістю функції розподілу ймовірностей (67)

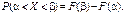Залежність (72) можна подати так:

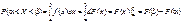
4. Функція розподілу ймовірностей неперервної випадкової величини має вигляд

(73)

Доведення. .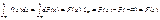

Якщо можливі значення неперервної випадкової величини належать лише інтервалу [а; b], то (74)

Приклад 2. Закон неперервної випадкової величини Х задано у вигляді:

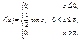
Знайти F(x) і побудувати графіки функцій f (x), F(x). Обчислити

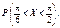
Розв’язання.Згідно із (74) маємо:

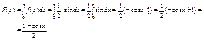
Отже, функція розподілу ймовірностей буде така:

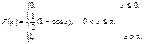
Графіки функцій f (x), F(x) зображені відповідно на рис. 29 і 30.

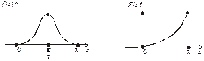
Рис. 29 Рис. 30

Імовірність події 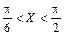можна обчислити згідно з (65) або (72). Застосуємо формулу (72):