Розв’язання. Отже, два закони розподілу мають однакові математичні сподівання, хоча можливі значення для випадкових величин Х і Y істотно різні

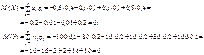
Отже, два закони розподілу мають однакові математичні сподівання, хоча можливі значення для випадкових величин Х і Y істотно різні. Із наведеного прикладу бачимо, що в разі рівності математичних сподівань (М (X) = М (Y) = 0) випадкові величини Х і Y мають тенденцію до коливань відносно М (X) та М (Y), причому Y має більший розмах розсіювання відносно М (Y), ніж випадкова величина Х відносно М (Х). Тому математичне сподівання називають центром розсіювання. Для вимірювання розсіювання вводиться числова характеристика, яку називають дисперсією.

Для визначення дисперсії розглядається відхилення випадкової величини Х від свого математичного сподівання (Х – М (Х))

Математичне сподівання такого відхилення випадкової величини Х завжди дорівнює нулю. Справді,

.

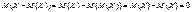Отже, відхилення не може бути мірою розсіювання випадкової величини.

Дисперсією випадкової величини Х називається математичне сподівання квадрата відхилення цієї величини

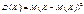. (86)

Для дискретної випадкової величини Х дисперсія

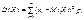; (87)

для неперервної

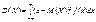. (88)

Якщо Х Î [а; b],

то 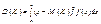. (89)