Початкові та центральні моменти
Узагальненими числовими характеристиками випадкових величин є початкові та центральні моменти.
Початковим моментом k-го порядку випадкової величини Х називають математичне сподівання величини Х k:
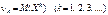 . (98)
. (98)
Коли 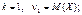 коли k = 2,
коли k = 2, 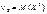 і т. д.
і т. д.
Для дискретної випадкової величини Х
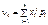 ; (99)
; (99)
для неперервної
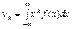 . (100)
. (100)
Якщо Х Î [а; b], то
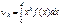 . (101)
. (101)
Центральним моментом k-го порядку називається математичне сподівання від (Х – М(Х))k:
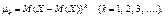 (102)
(102)
Коли 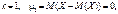
коли k = 2, 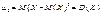 ;
;
коли k = 3, 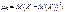
коли k = 4, 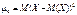 .
.
Для дискретної випадкової величини
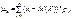 (103)
(103)
для неперервної
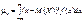 (104)
(104)
Якщо Х Î [а; b], то
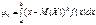 . (105)
. (105)
29. Асиметрія і ексцесТретій центральний момент характеризує асиметрію закону розподілу випадкової величини. Якщо m3 = 0, то випадкова величина Х симетрично розподілена відносно М (Х). Оскільки m3 має розмірність випадкової величини в кубі, то вводять безрозмірну величину — ко-
ефіцієнт асиметрії: 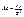 . (106)
. (106)
Центральний момент четвертого порядку використовується для визначення ексцесу, що характеризує плосковершинність, або гостровершинність щільності ймовірності f (x). Ексцес обчислюється за формулою 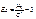 (107)
(107)
Зауважимо, що число 3 віднімається ось чому. Для центрального закону розподілу, так званого нормального закону, виконується рівність: 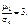 Отже, Еs = 0.
Отже, Еs = 0.
Для наочності при різних значеннях Аs, Es графіки f (x) зображені на рис. 57 i 58.
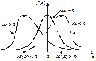
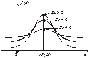
Рис. 57 Рис. 58
Приклад 13. Задано щільність імовірностей:
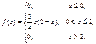
Обчислити Аs, Еs.Розв’язання.
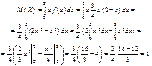
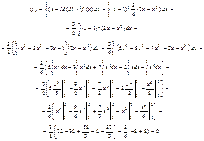
Оскільки m3 = 0, то і Аs = 0. Отже, можливі значення випадкової величини Х симетрично розподілені відносно М (Х) = 1. Для обчислення Еs необхідно знайти m4 і s.
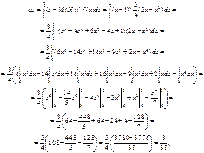
Дата добавления: 2014-11-29; просмотров: 1766;
