Властивості дисперсії
1. Якщо С — стала величина, то
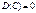. (90)
Справді
.
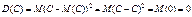2. 
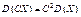. (91)
Маємо:
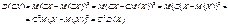
3. Якщо А і В — сталі величини, то
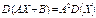. (92)
Адже
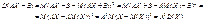
Дисперсію можна обчислити і за такою формулою:
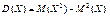(93)
Доведення. Згідно з (86) дістаємо:
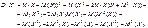
Для дискретної випадкової величини Х
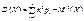; (94)
для неперервної
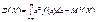. (95)
Якщо Х Î [а; b], то
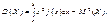(96)
Слід пам’ятати, що дисперсія не може бути від’ємною величиною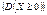 
.
Отже, дисперсія характеризує розсіювання випадкової величини відносно свого математичного сподівання. Якщо випадкова величина виміряна в деяких одиницях, то дисперсія вимірюватиметься в цих самих одиницях, але в квадраті.
Тому доцільно мати числову характеристику такої самої вимірності, як і випадкова величина. Такою числовою характеристикою є середнє квадратичне відхилення.
Середнім квадратичним відхиленням випадкової величини Х називають корінь квадратний із дисперсії:
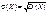. (97)
Приклад 8. Закон розподілу дискретної випадкової величини Х задано таблицею:
| хі | – 4 | – 2 | ||||
| рі | 0,1 | 0,2 | 0,3 | 0,2 | 0,1 | 0,1 |
Обчислити D (X), s (X).
Розв’язання. Згідно з (94) маємо:
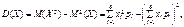
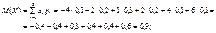
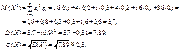
Дата добавления: 2014-11-29; просмотров: 1414;