Біном Ньютона. Трикутник Паскаля. Властивості біноміальних коефіцієнтів
З елементарної математики відомі формули скороченого множення:
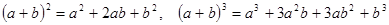 .
.
Ці формули можна записати і так:
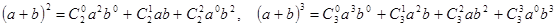 .
.
Очевидно, існує загальна закономірність.
Теорема 5.1.9. Справедлива рівність:
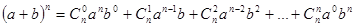 .
.
Цю рівність називають біномом Ньютона.
Біноміальні коефіцієнти можна подати у вигляді трикутної таблиці, яку називають трикутником Паскаля:
| п=1 | ||||||||||||
| п=2 | ||||||||||||
| п=3 | ||||||||||||
| п=4 | ||||||||||||
| п=5 | ||||||||||||
| ... | ||||||||||||
У п-му рядку трикутника Паскаля кожен коефіцієнт розкладу, крім двох крайніх, що дорівнюють 1, – це сума відповідних коефіцієнтів із попереднього рядка.
Узагальненням бінома Ньютона є наступна теорема:
Теорема 5.1.10 (поліноміальна теорема). Справедлива рівність:
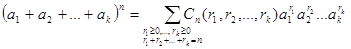 ,
,
де 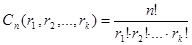 .
.
Числа 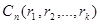 називають біноміальними коефіцієнтами.
називають біноміальними коефіцієнтами.
Властивості біноміальних коефіцієнтів:
1. 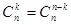 (випливає з теореми 4.1.6, якщо замінити у формулі k на (n–k), то (n–k) заміниться на (n– (n–k))=k).
(випливає з теореми 4.1.6, якщо замінити у формулі k на (n–k), то (n–k) заміниться на (n– (n–k))=k).
2. 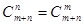 (формула симетрії).
(формула симетрії).
3. 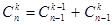 (формула додавання).
(формула додавання).
4. 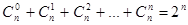 (
( 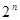 – кількість всіх розміщень з повтореннями з елементів 2-х типів).
– кількість всіх розміщень з повтореннями з елементів 2-х типів).
5. 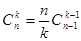 (формула винесення за дужки).
(формула винесення за дужки).
6. 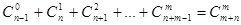 .
.
7. 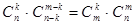 .
.
Дата добавления: 2014-12-22; просмотров: 7412;
