Тема 6.1. Теоретичні положення
Дискретне джерело інформації – це таке джерело, яке може виробити ( згенерувати ) за скінчений відрізок часу тільки скінчену множину повідомлень. Кожному такому повідомленню можна співставити відповідне число, та передавати ці числа замість пові-домлень.
Дискретне джерело інформації є достатньо адекватною інфор-маційною моделлю дискретних систем, а також неперервних систем, інформаційні сигнали про стан яких піддають аналого - цифровому пе-ретворенню; таке перетворення виконується в більшості сучасних автоматизованих систем управління.
Первинні характеристики дискретного джерела інформації – це алфавіт, сукупність ймовірностей появи символів алфавіту на виході дискретного джерела та тривалості символів.
Алфавіт – множина 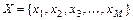 символів, які можуть з’явитися на виході дискретного джерела;
символів, які можуть з’явитися на виході дискретного джерела; 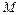 – потужність, тобто кількість різноманітних символів алфавіту.
– потужність, тобто кількість різноманітних символів алфавіту.
Якщо всі ймовірності, які визначають виникнення символів на виході джерела, не залежать від часу, джерело називають стаціонарним. Ми будемо розглядати тільки стаціонарні джерела та для скорочення замість “стаціонарне джерело” будемо всюди використовувати “джерело”.
Для опису джерел, які не мають пам’яті, достатньо мати значення безумовних імовірностей p(xi) виникнення символів xi , i = 1, 2, 3,…, M на його виході.
Більшість реальних джерел інформації є джерелами з пам’ят-тю. Розподіл ймовірностей виникнення чергового символу на виході дискретного джерела з пам’яттю залежить від того, які символи були попередніми. Таке джерело інформації називають марковським, оскільки процес появи символів на його виході адекватний ланцюгам Маркова; останні в свою чергу отримали таку назву на честь російського математика Маркова (старшого) Андрія Андрійовича (1856 – 1922), який заклав основи розділу теорії випадкових процесів.
Будемо говорити, що глибина пам’яті марковського дискретного джерела інформації дорівнює h, ( h ³ 0 ), якщо ймовірність появи чергового символу залежить тільки від h попередніх символів на виході цього джерела.
Кількість інформації – одне із основних понять теорії інформації, яка розглядає технічні аспекти інформаційних проблем, тобто вона дає відповіді на запитання такого типу: якою повинна бути ємність запам’ятовуючого пристрою для запису даних про стан деякої системи, якими повинні бути характеристики каналу зв’язку для передачі певного повідомлення тощо.
Кількісна оцінка інформації пов’язана з поняттям ентропії. Ентропія є мірою невизначеності, непрогнозованості ситуації. Зменшення ентропії, що відбулось завдяки деякому повідомленню, точно збігається з кількістю інформації, яка міститься в цьому повідомленні.
Для дискретного немарковського ( без пам’яті ) джерела інформації ентропія  визначається за таким виразом:
визначається за таким виразом:
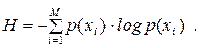
| (6.1) |
зазначимо, що  не залежить від того, якими є випадкові події або величини ( якщо
не залежить від того, якими є випадкові події або величини ( якщо  – випадкова величина ), а визначається тільки значеннями ймовірностей. Це означає, що ентропія є характеристикою розподілу ймовірностей.
– випадкова величина ), а визначається тільки значеннями ймовірностей. Це означає, що ентропія є характеристикою розподілу ймовірностей.
Значення  показує, яку кількість інформації в середньому дає поява одного символу на виході дискретного джерела інформації. Ця міра запропонована американським математиком і інженером Клодом Шенноном.
показує, яку кількість інформації в середньому дає поява одного символу на виході дискретного джерела інформації. Ця міра запропонована американським математиком і інженером Клодом Шенноном.
Якщо основа логарифма в (6.1) дорівнює двом, то одиниці вимірювання H, а також кількості інформації називають бітами або двійковими одиницями.
Ентропія дискретного розподілу ймовірностей завжди невід’ємна і набуває максимального значення H max , коли всі 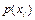 мають однакові значення:
мають однакові значення:
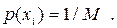
| (6.2) |
В цьому разі маємо міру кількості інформації, яку ще до Шеннона було запропоновано англійським математиком Р.Хартлі. Підставимо (6.2) в (6.1), отримаємо
H = H max = log 2 M . (6.3)
Значення H max збігається з кількістю двійкових комірок па-м’яті, які необхідно мати, щоб зафіксувати за допомогою двійкового коду інформацію про один із M можливих станів системи, або про символ, що з’явиться на виході дискретного джерела інформації.
Ентропія дорівнює нулю, якщо ймовірність появи одного з символів є одиниця ( при цьому, звичайно, ймовірність появи будь - якого іншого символа буде дорівнювати нулю ); в такій ситуації невизначеність відсутня.
Продуктивність 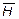 джерела інформації – це кількість інформації, що виробляється джерелом за одиницю часу:
джерела інформації – це кількість інформації, що виробляється джерелом за одиницю часу:
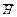 = H / t , = H / t ,
| (6.4) |
де  – середня тривалість символу,
– середня тривалість символу, 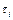 – тривалість символу
– тривалість символу 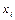 .
.
Надмірність ( надлишок ) R дискретного джерела інформації дає відносну оцінку використання потенційних можливостей джерела з алфавітом заданої потужності 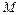 :
:
| R = | H max – H | = | log 2 M – H | = 1 – | H | (6.5) | |
| H max | log 2 M | log 2 M | . |
Надмірність може приймати значення від 0 до 1. Вона дорівнює нулю, якщо H = H max ; в цьому випадку дискретне джерело інформації буде виробляти максимально можливий інформаційний потік. Із першої теореми Шеннона виходить, що при застосуванні ефективного кодування надмірність може бути зведена практично до нуля, внаслідок чого об’єм повідомлення буде зменшено майже в 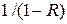 разів.
разів.
Ентропія, продуктивність та надмірність – інтегральні інформаційні характеристики дискретного джерела інформації.
Розглянемо сукупність двох дискретних немарковських джерел інформації з алфавітами 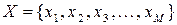 та
та 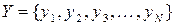 , ентропії яких позначимо відповідно як
, ентропії яких позначимо відповідно як 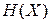 та
та 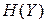 . Для спрощення будемо вважати, що всі символи мають однакові тривалості, а зміни символів на виходах обох джерел відбуваються одночасно. Ентропії кожного з джерел знаходяться за виразом (6.1) через безумовні ймовірності появи символів
. Для спрощення будемо вважати, що всі символи мають однакові тривалості, а зміни символів на виходах обох джерел відбуваються одночасно. Ентропії кожного з джерел знаходяться за виразом (6.1) через безумовні ймовірності появи символів 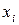 та
та 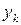 . Якщо джерела є статистично залежними, то поява, наприклад, символу
. Якщо джерела є статистично залежними, то поява, наприклад, символу  на виході першого джерела дасть розподіл умовних імовірностей
на виході першого джерела дасть розподіл умовних імовірностей 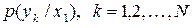 виникнення символів
виникнення символів 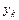 на виході другого джерела, який у загальному випадку буде відрізнятися від розподілу умовних ймовірностей
на виході другого джерела, який у загальному випадку буде відрізнятися від розподілу умовних ймовірностей 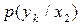 при умові появи на виході першого джерела символу
при умові появи на виході першого джерела символу  . Звичайно, в такій ситуації ентропія другого джерела буде залежити від того, який символ з’явився на виході першого джерела. Знаходиться ця ентропія через умовні ймовірності:
. Звичайно, в такій ситуації ентропія другого джерела буде залежити від того, який символ з’явився на виході першого джерела. Знаходиться ця ентропія через умовні ймовірності:
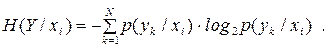
| (6.6) |
Вона має назву умовної частинної ентропії та характеризує невизначеність символів на виході другого джерела при умові, що на виході першого з’явився символ  . Якщо
. Якщо 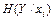
 усереднити по всіх
усереднити по всіх  , то отримаємо середню або повну умовну ентропію:
, то отримаємо середню або повну умовну ентропію:
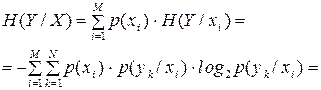
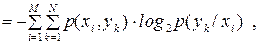
| (6.7) |
де 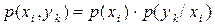 – ймовірність сумісної появи символів
– ймовірність сумісної появи символів  та ykна виходах відповідно першого та другого джерела.
та ykна виходах відповідно першого та другого джерела.
Ця ентропія характеризує в середньому невизначеність символів на виході другого джерела, якщо є можливість спостерігати за появою символів на виході першого джерела.
Аналогічно визначається частинна 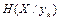 та середня ( пов-на )
та середня ( пов-на ) 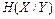 умовні ентропії для першого джерела.
умовні ентропії для першого джерела.
Якщо дискретні джерела статистично незалежні, то
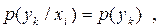 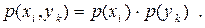
| (6.8) |
В цьому випадку
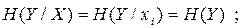
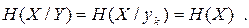
| (6.9) |
Середня умовна ентропія 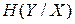 не може перевищувати безумовну ентропію
не може перевищувати безумовну ентропію 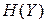 ; частинна умовна ентропія
; частинна умовна ентропія 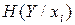 може бути більша, ніж
може бути більша, ніж 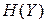 . Середня умовна ентропія буде дорівнювати нулю, якщо поява будь якого символу xi, i = 1,2,3,…, M на виході першого джерела однозначно визначає символ на виході другого джерела. Тобто, спостерігаючи за виникненням символів на виході першого джерела, будемо мати повну інформацію про послідовність символів на виході другого джерела навіть за умов недоступності цього виходу для спостереження.
. Середня умовна ентропія буде дорівнювати нулю, якщо поява будь якого символу xi, i = 1,2,3,…, M на виході першого джерела однозначно визначає символ на виході другого джерела. Тобто, спостерігаючи за виникненням символів на виході першого джерела, будемо мати повну інформацію про послідовність символів на виході другого джерела навіть за умов недоступності цього виходу для спостереження.
Таким чином для середньої умовної 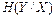 та безумовної
та безумовної 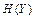 ентропій мають місце співвідношення:
ентропій мають місце співвідношення:
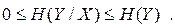
| (6.10) |
Для двох визначених вище дискретних джерел можна розрахувати сумісну ентропію 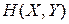 сукупності символів
сукупності символів 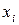 ,
, 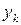 або ентропію об'єднання ансамблей
або ентропію об'єднання ансамблей 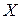 та
та 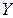 :
:
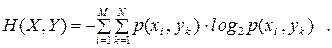
| (6.11) |
Для обчислення 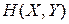 слід мати набір або матрицю ймовірностей
слід мати набір або матрицю ймовірностей 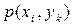 сумісної появи
сумісної появи 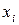 та
та 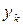
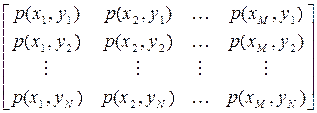 . (6.12)
. (6.12)
Сума елементів 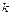 -го рядка цієї матриці дорівнює безумовній імовірності
-го рядка цієї матриці дорівнює безумовній імовірності 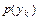 появи символу
появи символу 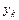 на виході другого джерела, а сума елементів
на виході другого джерела, а сума елементів  -го стовпця – безумовній ймовірності
-го стовпця – безумовній ймовірності 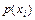 появи символу
появи символу  на виході першого джерела:
на виході першого джерела:
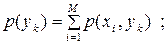 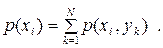
| (6.13) |
Маючи безумовні ймовірності 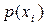 та
та 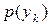 появи символів
появи символів 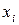 та
та 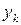 на виході кожного з джерел, а також ймовірності
на виході кожного з джерел, а також ймовірності 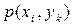 сумісної їх появи, можна обчислити умовні ймовірності
сумісної їх появи, можна обчислити умовні ймовірності 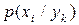 та
та 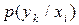 , користуючись виразом:
, користуючись виразом:
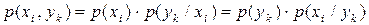 , ,
| (6.14) |
а далі за виразом (6.7) знайти умовні ентропії 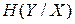 та
та 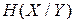 . Тобто матриця (6.12) дає необхідні дані для обчислення ентропій
. Тобто матриця (6.12) дає необхідні дані для обчислення ентропій 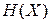 ,
, 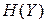 кожного з джерел та умовних ентропій
кожного з джерел та умовних ентропій 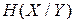 ,
, 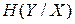 .
.
Всі вище перелічені ентропії можна також отримати із матриць умовних ймовірностей 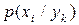 або
або 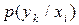 та необхідної кількості безумовних ймовірностей
та необхідної кількості безумовних ймовірностей 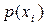 та
та 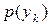 .
.
Ентропію 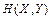 системи двох джерел, користуючись виразом (6.14), подамо у вигляді:
системи двох джерел, користуючись виразом (6.14), подамо у вигляді:
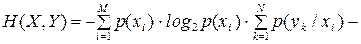
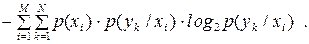
| (6.15) |
Перша складова з урахуванням того, що
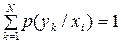 , ,
|
є ентропією 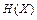 першого джерела, друга збігається з виразом (6.7) для умовної ентропії. Тобто
першого джерела, друга збігається з виразом (6.7) для умовної ентропії. Тобто
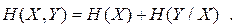
| (6.16) |
Аналогічно можна показати, що
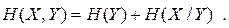
| (6.17) |
Якщо джерела статистично незалежні, то із виразу (6.9) виходить
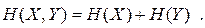
| (6.18) |
У загальному випадку
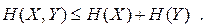
| (6.19) |
Для системи, що складається з 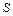 джерел з алфавітами
джерел з алфавітами 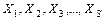 , ентропія визначається так:
, ентропія визначається так:
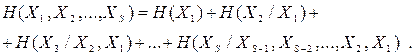
| (6.20) |
Звичайно, як і для двох джерел, має місце співвідношення
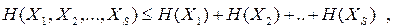
| (6.21) |
де рівність має місце, коли всі джерела статистично незалежні.
Звернемось знову до системи двох дискретних джерел. Спостерігаючи за виникненням символів на виході одного із джерел, наприклад першого, в загальному випадку будемо отримувати певну кількість інформації про появу символів на виході другого джерела. Ця інформація 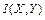 в розрахунку на один символ буде дорівнювати зменшенню ентропії другого джерела. Оскільки початкова або апріорна ентропія другого джерела ( тобто ентропія, яка мала місце до спроби, де під спробою будемо розуміти появу символу на виході першого джерела, який є доступним ) дорівнює
в розрахунку на один символ буде дорівнювати зменшенню ентропії другого джерела. Оскільки початкова або апріорна ентропія другого джерела ( тобто ентропія, яка мала місце до спроби, де під спробою будемо розуміти появу символу на виході першого джерела, який є доступним ) дорівнює 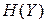 , а залишкова або апостеріорна ( після спроби ) ентропія буде
, а залишкова або апостеріорна ( після спроби ) ентропія буде 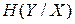 , то
, то
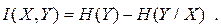
| (6.22) |
Ця величина показує, яка кількість інфомації в середньому міститься в одному символі першого джерела про виникнення символів на виході другого джерела.
Користуючись виразами для безумовної та умовної ентропій, після деяких перетворень можна отримати:

| (6.23) |
Крім того, враховуючи (6.16) та (6.17), будемо мати такі інтерпретації для  :
:
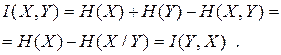
| (6.24) |
Тобто кількість інформації, що містить в середньому символ на виході першого джерела про виникнення символів на виході другого джерела, дорівнює кількості інформації, яка міститься в середньому в символі на виході другого джерела про виникнення символів на виході першого. Через це 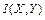 має назву повної взаємної інформації. Аналіз виразів (6.22), (6.23), (6.24) показує, що рівність повної взаємної інформації нулю є необхідною і достатньою умовою статистичної незалежності джерел.
має назву повної взаємної інформації. Аналіз виразів (6.22), (6.23), (6.24) показує, що рівність повної взаємної інформації нулю є необхідною і достатньою умовою статистичної незалежності джерел.
Користуючись поняттям умовної ентропії, можна отримати вираз для обчислення ентропії  джерела з пам’яттю, яке має алфавіт
джерела з пам’яттю, яке має алфавіт 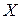 . Якщо глибина пам’яті такого джерела дорівнює
. Якщо глибина пам’яті такого джерела дорівнює 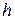 , а потужність алфавіту
, а потужність алфавіту 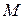 , то можна вважати, що перед генерацією чергового символу джерело знаходиться в одному з
, то можна вважати, що перед генерацією чергового символу джерело знаходиться в одному з 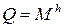 станів, де під станом розуміємо одну з можливих послідовностей попередніх символів довжиною
станів, де під станом розуміємо одну з можливих послідовностей попередніх символів довжиною 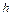 на його виході.
на його виході.
Тоді частинна умовна ентропія 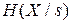 при умові, що джерело перебуває в s-му стані
при умові, що джерело перебуває в s-му стані
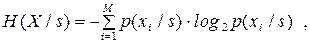
| (6.25) |
де 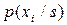 – умовна ймовірність появи символу
– умовна ймовірність появи символу  , якщо джерело перебуває в s-му стані.
, якщо джерело перебуває в s-му стані.
Усереднюючи 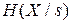 по усіх станах, отримаємо вираз для ентропії марковського джерела:
по усіх станах, отримаємо вираз для ентропії марковського джерела:
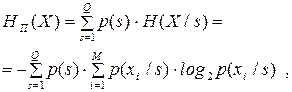
| (6.26) |
тут  – ймовірність перебування джерела в s-му стані.
– ймовірність перебування джерела в s-му стані.
Якщо статистичні зв’язки мають місце лише між двома суміжними символами (тобто джерело має глибину пам’яті 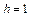 ), стан джерела визначається тільки попереднім символом
), стан джерела визначається тільки попереднім символом  ; в цьому разі ентропія
; в цьому разі ентропія 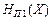 джерела обчислюється за таким виразом:
джерела обчислюється за таким виразом:
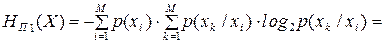
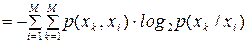 . .
| (6.27) |
Для джерела з глибиною пам’яті 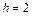 стан визначається парою символів
стан визначається парою символів 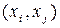 , а ентропія:
, а ентропія:
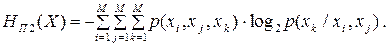
| (6.28) |
Аналогічно можна отримати вирази для ентропій марковських джерел при більш глибоких статистичних зв’язках.
Дата добавления: 2014-12-22; просмотров: 2159;
