Задача 6.2.3
Матриця ймовірностей сумісної появи символів на виходах двох немарковських джерел з алфавітами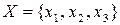 
та 
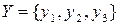має вигляд:
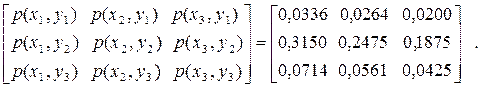
Визначити, яке з джерел має більшу ентропію та чи є джерела статистично незалежними.
Розв’язання. Для відповіді на перше запитання розрахуємо, користуючись виразами (1.13), безумовні ймовірності появи символів на
виходах першого та другого джерел:
p(x1) = 0,0336 + 0,3150 + 0,0714 = 0,42 ;
p(x2) = 0,0264 + 0,2475 + 0,0561 = 0,33 ;
p(x3) = 0,0200 + 0,1875 + 0,0425 = 0,25 ;
p(y1) = 0,0336 + 0,0264 + 0,0200 = 0,08 ;
p(y2) = 0,3150 + 0,2475 + 0,1875 = 0,75 ;
p(y3) = 0,0714 + 0,0561 + 0,0425 = 0,17 .
Тепер можемо знайти ентропії джерел за виразом (6.1):
|
Таким чином, джерело з алфавітом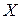 
має більшу ентропію, ніж джерело з алфавітом 
.
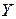Відповідь на друге запитання можна отримати різними способами. По-перше, оскільки вже відомі значення ентропій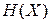 
та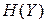 
, доцільно перевірити, чи виконується рівність (6.18). Для цього розрахуємо сумісну ентропію 
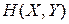. Підставивши чисельні значення ймовірностей у вираз (6.11), отримаємо:
|
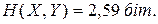
Оскільки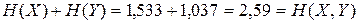 
,джерела є статистично незалежними.
Другий спосіб базується на перевірці виконання співвідношень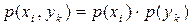 
для всіх пар символів:
p(x1) × p(y1) = 0,42×0,08 = 0,0336 ;
p(x2) × p(y1) = 0,33×0,08 = 0,0264 ;
p(x3) × p(y1) = 0,25×0,08 = 0,0200 ;
p(x1) × p(y2) = 0,42×0,75 = 0,3150 ;
p(x2) × p(y2) = 0,33×0,75 = 0,2475 ;
p(x3) × p(y2) = 0,25×0,75 = 0,1875 ;
p(x1) × p(y3) = 0,42×0,17 = 0,0714 ;
p(x2) × p(y3) = 0,33×0,17 = 0,0561 ;
p(x3) × p(y3) = 0,25×0,17 = 0,0561 .
Як і слід було очікувати, розраховані ймовірності цілком збігаються із відповідними значеннями ймовірностей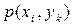 
сумісної появи символів, що наведені в умовах задачі.
Найбільш універсальним способом оцінки статистичної залежності джерел є обчислення повної взаємної інформації 
. Аналізуючи вираз (6.23), легко зрозуміти, що для джерел цієї задачі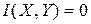 
,оскільки для усіх пар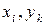 
|
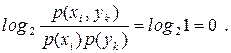
Ще один спосіб розв’язання задачі базується на аналізі матриці умовних імовірностей. Розрахуємо, наприклад, умовні ймовірності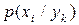 
, користуючись виразом 
:
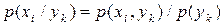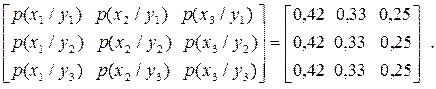
Всі елементи кожного стовпця однакові і дорівнюють безумовній ймовірності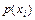 
появи відповідного символу 
. Це означає, що ймовірність появи символу на виході першого джерела не залежить від символу на виході другого джерела. Можна переконатись, що i в матриці умовних ймовірностей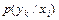 
всі елементи кожного стовпця будуть однаковими і дорівнювати 
.
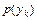Дата добавления: 2014-12-22; просмотров: 712;