Задача 6.2.5
Маємо три дискретних немарковських джерела з алфавітами  Ймовірності сумісної появи символів мають такі значення:
Ймовірності сумісної появи символів мають такі значення:
p ( x1, y1, z1 ) = 0,048;
p ( x1, y1, z2 ) = 0,012;
p ( x1, y2, z1 ) = 0,072;
p ( x1, y2, z2 ) = 0,162;
p ( x2, y1, z1 ) = 0,272;
p ( x2, y1, z2 ) = 0,068;
p ( x2, y2, z1 ) = 0,300;
p ( x2, y2, z2 ) = 0,060.
Знайти ентропії кожного з джерел, системи трьох джерел, а також повну взаємну інформацію для кожної пари джерел.
Розв’язання. Щоб знайти ентропію кожного з джерел, розрахуємо ймовірності появи символів на виході джерел згідно з виразами:
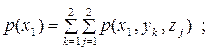 
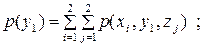 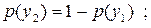
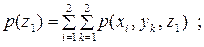 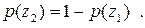
|
Маємо такі значення:
p ( x1) = 0,3; p ( x2) = 0,7; p ( y1) = 0,4;
p ( y2) = 0,6; p ( z1) = 0,692; p ( z2) = 0,308.
Знаходимо ентропії джерел:
H(X) = 1,8813 біт ; H(Y) = 0,971 біт ; H(Z) = 0,8909 біт .
Щоб обчислити повну взаємну інформацію, знайдемо ентропії 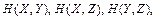 для чого розрахуємо ймовірності сумісної появи пар символів, користуючись виразами типу:
для чого розрахуємо ймовірності сумісної появи пар символів, користуючись виразами типу:

|
Маємо
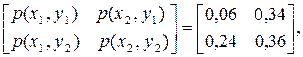
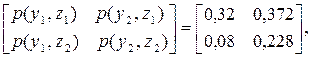
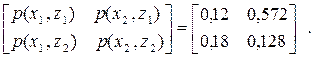
|
За виразом (1.11) обчислюємо ентропії кожної із систем двох джерел:
H(X,Y ) = 1,7975 біт ; H(X,Z) = 1,653 біт ; H(Y,Z) = 1,8345 біт .
Тепер знаходимо значення повної взаємної інформації для всіх пар джерел:
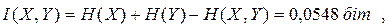
|
Аналогічно
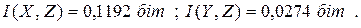
|
Для обчислення ентропії системи трьох джерел скористуємось виразом (6.20), коли 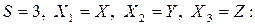
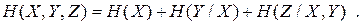
|
Із виразу (1.16) отримаємо
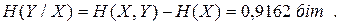
|
Щоб знайти H(Z/Y,X), необхідно розрахувати умовні ймовірності типу 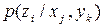 . Для цього скористаємось виразами:
. Для цього скористаємось виразами:
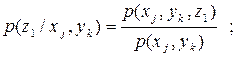
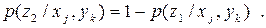
Отримаємо
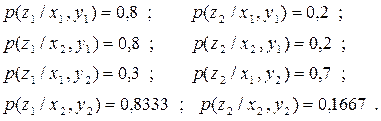
|
Далі знаходимо частинні умовні ентропії
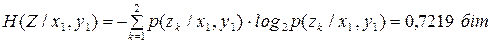 ,
,
аналогічно
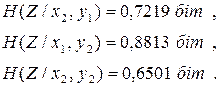
|
Тепер обчислимо повну умовну ентропію:
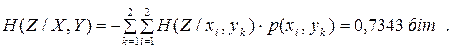
Нарешті
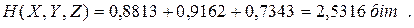
|
Дата добавления: 2014-12-22; просмотров: 980;
