Задача 6.2.6
Марковське дискретне джерело інформації з алфавітом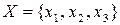 
та глибиною пам’яті 
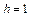описується такою матрицею умовних ймовірностей 
виникнення символу xi при умові, що йому передував символ xk :
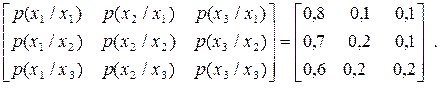
| (6.29) |
Обчислити ентропію такого джерела.
Розв’язання. Щоб розрахувати ентропію марковського джерела, необхідно знати безумовні ймовірності 
появи відповідних символів на виході джерела. Їх можна отримати, скористувавшись рівняннями:
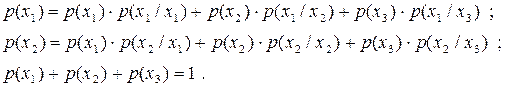
Підставивши сюди значення умовних ймовірностей з матриці (1.29) та дещо спростивши, будемо мати систему лінійних рівнянь:
|
Розв'язання системи дає:
|
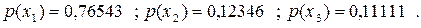
Тепер можна скористуватись безпосередньо виразом (6.27) , або ж обчислити частинні умовні ентропії для кожного стану джерела, а потім знайти ентропію марковського джерела, як математичне сподівання вищезгаданих частинних умовних ентропій. Кожна частинна умовна ентропія 
– це ентропія розподілу умовних імовірностей, розташованих в одному з рядків матриці (6.29).
Обравши другий шлях, будемо мати:
| |
| |
| |
Дата добавления: 2014-12-22; просмотров: 838;