Задача 1.2.8

Маємо два немарковських дискретних джерела інформації з алфавітами Ймовірності появи символів на виході першого джерела

Значення умовних ймовірностей 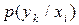виникнення символу 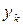на виході другого джерела при умові, що на виході першого з'явився символ 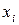, є такими:

. (6.33)

Розрахувати ентропії кожного з джерел, системи двох джерел та повну взаємну інформацію.

Розв'язання. Скористуємось формулою повної ймовірності

для визначення ймовірностей появи символів на виході джерела з алфавітом

Отримані значення збігаються із значеннями ймовірностей 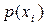. Висновок про це можна було зробити, аналізуючи матрицю (6.33). Кожний рядок і кожний стовпець має у своєму складі по одній одиниці. Це свідчить, що між символами існує взаємно-однозначний зв'язок. Тому

H(X)= H(Y) = 1,28 біт .

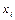Для визначення та розрахуємо ймовірності сумісної появи символів та 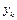за виразом (6.14):

Тепер неважко пересвідчитись (зробіть це самостійно), що

H(X,Y) = I(X,Y ) = H(X) = H(Y) = 1,28 біт .

Задачі

6.3.1. Отримати чисельні значення ентропії, продуктивності та надмірності немарковського дискретного джерела інформації з алфавітом X потужності M = 4 .Значення ймовірностей p(x_i) виникнення символів та їх тривалостей t_i( в мілісекундах, мс ) для різних варіантів наведені у таблиці 6.3.1.

Таблиця 6.3.1

№ варіанта	p(x₁)	p(x₂)	p(x₃)	p(x₄)	t₁	t₂	t₃	t₄
	0,33	0,08	0,15	0,44	1,2	0,2	0,8	0,5
	0,21	0,16	0,03	0,6	5,4	1,5	2,3	1,2
	0,15	0,27	0,34	0,24
	0,05	0,08	0,11	0,76	8,6	3,4	5,8	0,9
	0,62	0,28	0,04	0,06	0,3	0,4	0,6	0,8
	0,17	0,41	0,23	0,19	2,6	1,1	0,5	7,3
	0,55	0,15	0,06	0,24	3,3	5,1	1,2	1,2
	0,08	0,35	0,27	0,30	0,1	0,3	0,5	0,8
	0,22	0,33	0,05	0,40	2,2	1,8	0,5	3,0
	0,62	0,12	0,08	0,18	1,8	0,8	0,6	0,5
	0,26	0,14	0,50	0,10	3,7	2,1	1,2	1,5
	0,14	0,33	0,27	0,26	0,2	0,1	0,5	1,5
	0,18	0,03	0,64	0,15	2,5	1,4	0,7	2,2
	0,37	0,18	0,06	0,39
	0,25	0,15	0,33	0,27	1,8	1,2	0,8	0,5
	0,09	0,44	0,28	0,19
	0,66	0,15	0,15	0,04	3,4	5,8	1,3	2,5
	0,22	0,05	0,16	0,57	0,5	0,3	0,2	0,8
	0,53	0,24	0,15	0,08	7,6	2,1	1,5	8,3
	0,18	0,22	0,25	0,35	2,8	3,5	4,8	1,3

1.3.2. Маємо два немарковських дискретних джерела інформації з алфавітами X = {x₁, x₂, x₃} та Y = {y₁, y₂}. Чисельні значення ймовірностей p(x_i, y_k) сумісного виникнення символів на виходах джерел для різних варіантів наведені у таблиці 1.3.2. Чому дорівнює ентропія системи цих двох джерел? Яке з цих джерел має більшу надмірність? Чи є джерела статистично незалежними?

Таблиця 1.3.2

№ варіанта	p ( x₁, y₁)	p ( x₁, y₂)	p ( x₁, y₃)	p ( x₂, y₁)	p ( x₂, y₂)	p ( x₂, y₃)
	0,15	0,08	0,25	0,30	0,16	0,06
	0,12	0,04	0,24	0,18	0,06	0,36
	0,33	0,11	0,06	0,06	0,11	0,33
	0,05	0,08	0,11	0,36	0,25	0,15
	0,22	0,28	0,04	0,06	0,15	0,25
	0,17	0,21	0,23	0,12	0,08	0,19
	0,24	0,03	0,03	0,56	0,07	0,07
	0,08	0,08	0,30	0,12	0,12	0,30
	0,12	0,33	0,05	0,24	0,15	0,11
	0,09	0,18	0,18	0,11	0,22	0,22
	0,22	0,09	0,18	0,18	0,11	0,22
	0,14	0,28	0,08	0,26	0,14	0,10
	0,42	0,12	0,06	0,28	0,08	0,04
	0,03	0,18	0,26	0,26	0,12	0,15
	0,15	0,15	0,43	0,08	0,08	0,11
	0,21	0,08	0,28	0,15	0,12	0,16
	0,16	0,05	0,04	0,24	0,06	0,45
	0,02	0,05	0,43	0,02	0,33	0,15
	0,15	0,05	0,05	0,45	0,15	0,15
	0,06	0,03	0,01	0,54	0,27	0,09

6.3.3.Марковське дискретне джерело інформації має алфавіт X = {x₁, x₂}. Статистичні зв’язки розповсюджуються тільки на суміжні символи ( тобто глибина пам’яті h = 1). Чисельні значення умовних ймовірностей p(x_i/x_k) та тривалостей символів t_i(в мі-лісекундах, мс ) для різних варіантів наведені у таблиці 6.3.3. Отримати чисельні значення ентропії, продуктивності та надмірності джерела.

Таблиця 6.3.3

№ варіанта	p ( x ₁/ x ₁)	p ( x ₂/ x ₁)	p( x₁/ x₂)	p ( x ₂/ x ₂)	t₁	t₂
	0,53	0,47	0,25	0,75	0,1	0,3
	0,22	0,78	0,43	0,57	3,3	5,1
	0,15	0,85	0,64	0,36	2,6	1,1
	0,92	0,08	0,84	0,16	0,3	0,4
	0,62	0,38	0,24	0,76	2,3	1,4
	0,59	0,41	0,61	0,39	8,6	3,4
	0,35	0,65	0,16	0,84
	0,55	0,45	0,97	0,03	5,4	1,5
	0,12	0,88	0,35	0,65	1,2	0,2
	0,58	0,42	0,82	0,18	2,8	3,5
	0,16	0,84	0,52	0,48	7,6	2,1
	0,64	0,36	0,83	0,17	0,5	0,3
	0,18	0,82	0,44	0,56	2,5	1,4
	0,80	0,20	0,71	0,29	3,4	5,8
	0,25	0,75	0,33	0,67
	0,55	0,45	0,11	0,89	0,6	1,8
	0,21	0,79	0,16	0,84	1,8	1,2
	0,95	0,05	0,63	0,37
	0,23	0,77	0,51	0,49	0,2	0,1
	0,75	0,25	0,84	0,16	3,7	2,1

6.3.4. Маємо два немарковських дискретних джерела інформації з алфавітами X = {x₁, x₂, x₃} та Y = {y₁, y₂}. Чисельні значення безумовних p( y_k) та умовних p( y_k/ x_i) ймовірностей виникнення символів на виході джерела з алфавітом Y відомі та для різних варіантів наведені у таблиці 6.3.4. Отримати чисельні значення ентропії H ( X , Y ) системи цих двох джерел та повної взаємної інформації I ( X , Y ). Яке з цих джерел має більшу надмірність?

Таблиця 6.3.4

№ варіанта	p( y₁)	p( y₂)	p( y₃)
	0,37	0,594	0,036
	0,498	0,240	0,262
	0,5	0,24	0,26
	0,575	0,29	0,135
	0,304	0,29	0,406
	0,479	0,348	0,173
	0,206	0,168	0,626
	0,266	0,466	0,268
	0,424	0,136	0,44
	0,656	0,188	0,156
	0,257	0,504	0,239
	0,412	0,202	0,386
	0,181	0,449	0,37
	0,368	0,178	0,454
	0,532	0,082	0,386
	0,236	0,328	0,436
	0,483	0,221	0,296
	0,312	0,348	0,34
	0,168	0,286	0,546
	0,444	0,225	0,331

<6364 65 66 67 68 69 >

Дата добавления: 2014-12-22; просмотров: 1404;