Задача 7.2.3

Побудувати ефективні нерівномірні коди Хаффмена та Шеннона-Фано для кодування символів немарковського джерела з алфавітом 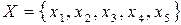; ймовірності виникнення символів мають такі значення: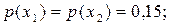

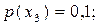
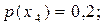
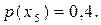
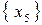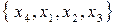Розв’язання.Спочатку побудуємо нерівномірний код за методикою Шеннона-Фано. Згідно з алгоритмом упорядковуємо символи по незростанню ймовірностей та виконуємо перший поділ множини символів на дві підмножини. Однак цей поділ не є однозначним: перший варіант поділу – на та , другий варіант – н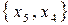а та 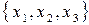. Обидва варіанти дають однакові суми ймовірностей появи символів підмножин: 0,4 та 0,6. Таблиці 7.3 та 7.4 відображають побудову кодів Шеннона-Фано для двох варіантів.

Таблиця 7.3

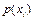
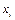
		Кодова комбінація		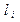Номер поділу
0,4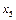
0,2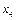
0,15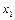
0,15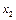
0,1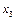

Таблиця 7.4

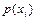
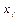
		Кодова комбінація		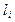Номер поділу
0,4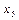
0,2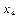
0,15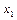
0,15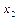
0,1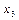

Середня довжина кодової комбінації для першого варіанта

;

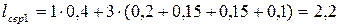для другого

.

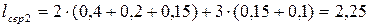Зрозуміло, що хоча б один з цих кодів (той, що має більшу середню довжину кодової комбінації) не є оптимальним. Таким чином методика Шеннона-Фано не гарантує оптимальності коду.

Для отримання коду Хаффмена будуємо кодове дерево (рис.7.4), приписуємо гілкам символи алфавіту двійкового коду та записуємо кодові комбінації: 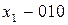; ; 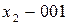; ; 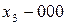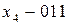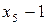. Символи двійкового алфавіту приписувались гілкам дерева цілеспрямовано таким чином, щоб код цілком збігався з першим варіантом коду, побудованим за методикою Шеннона-Фано. Цей код є оптимальним з середньою довжиною кодової комбінації 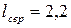. Ентропія джерела H(X) = 2,146 біт. Відносна різниця середньої довжини оптимального ефективного коду та ентропії джерела дорівнює

[ ( 2,2 – 2,146 ) / 2,146 ] ´ 100% = 2,52%.

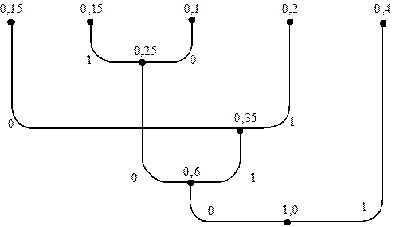
Рис. 2.4. Кодове дерево до задачі 2.2.3