Задача 7.2.5
Розробити ефективний код для кодування послідовності символів на виході немарковського дискретного джерела інформації з алфавітом {A,B,C} та ймовірностями появи символів p(A) = 0,15; p(B) = 0,1; p(C) = 0,75. Відносна різниця між середньою довжиною кодової комбінації та ентропією джерела не повинна перевищувати 2%. Закодувати таким кодом послідовнісь довжиною у 30 символів
САССССССССССВССАССССВССВСААССС,
яку згенерувало джерело.
Розв’язання.Зменшення середньої довжини кодової комбінації на один символ джерела можна досягти, якщо будувати ефективний код для укрупненого алфавіту. Хоча ефективний нерівномірний код розробляється на основі статистичних характеристик джерела, знання цих характеристик не дає можливості розрахувати середню довжину кодової комбінації без побудови коду.
Тому шлях розв’язання задачі повинен бути таким. Послідовно укрупнюємо алфавіт; для кожного укрупнення будуємо нерівномірний ефективний код, розраховуємо середню довжину кодової комбінації на один символ джерела та перевіряємо, чи задовольняються вимоги до неї. Процес укрупнення припиняємо, як тільки ці вимоги задовольняються.
Будуємо ефективний код для кодування окремих символів джерела. На рис. 7.5 зображено кодове дерево, що відповідає коду Хаффмена для такого джерела. Аналізуючи шляхи від кореневого вузла до кінцевих вузлів, знаходимо, що для символу A довжина кодової комбінації дорівнює 2, для символу B – 2, для символу С – 1. Середня довжина lcep (1) = 1 кодової комбінації для кодування по одному символу джерела
lcep (1) = 2× p(A) + 2× p(B) + 1× p(C) = 2(0,15+0,1)+1×0,75 = 1,25.
Ентропія джерела
H = – p(A)×log2 p(A) – p(B)×log2 p(B) – p(C)×log2 p(C) = 1,054 біт.
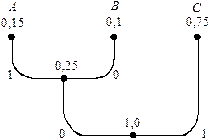
Рис. 7.5. Кодове дерево для символів джерела задачі 7.2.5
Відносна різниця між середньою довжиною кодової комбінації та ентропією джерела становить
[(1,25 – 1,054) / 1,054] ´ 100% = 18,6%,
що не задовольняє умовам задачі.
Укрупнюємо алфавіт, об’єднуючи по два символи джерела, знаходимо ймовірності появи укрупнених символів-слів та будуємо ефективний код для такого алфавіту. Оскільки джерело не має пам’яті, ймовірності появи слів отримаємо як добуток безумовних ймовірностей появи відповідних символів джерела, наприклад p(AB)= = p(A)×p(B). Кодове дерево для цього варіанту зображено на рис.2.6. Результати побудови коду Хаффмена у відповідності з цим деревом наведені у табл.7.8.
Середня довжина кодової комбінації в розрахунку на один символ вихідного джерела має значення
lcep ( 2 ) = [1´0,5625+3´(2´0,1125+0,075)+4´0,075+6´(0,0225+
+2´0,015+0,01)]/2 = 1,069.
Рис. 7.6. Кодове дерево для укрупненого по два 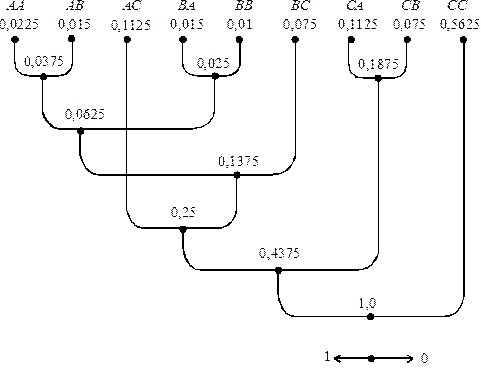
символи алфавіту джерела задачі 7.2.5
Таблиця 7.8
| Слово джерела (СД ) | Ймовірність появи СД | Кодова комбінація (КК) | Довжина КК |
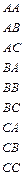
| 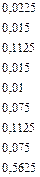
| 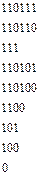
| 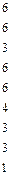
|
Відносна різниця між lcep ( 2 ) та ентропією джерела
[(1,069 – 1,054) / 1,054] ´ 100% = 1,4%,
що менше, ніж 2%, тобто такий код задовольняє вимогам.
Щоб закодувати послідовність, яку виробило джерело, поділяємо її на слова довжиною по 2 символи та застосовуємо для цих слів код табл.7.8. В результаті маємо
1010000011001010011001001011110.
Довжина двійкової послідовності дорівнює 31.
Задача 7.2.6
Розробити марковський алгоритм кодування для марковського джерела з алфавітом {A,B,C} та глибиною пам’яті h = 1. Умовні ймовірності виникнення символів задаються матрицею
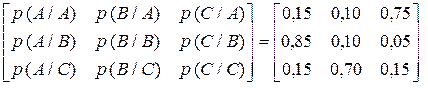 . .
|
Знайти відносну різницю між середньою довжиною кодової комбінації ефективного коду та ентропією джерела. Закодувати послідовність довжиною у 30 символів
АСАСВАСВАСВАВАВВАСВВАССАСВАСВА,
яку згенерувало джерело.
Розв’язання. Оскільки глибина пам’яті h = 1, кількість Q станів джерела дорівнює потужності його алфавіт, тобто Q = 3. Для кожного стану, який визначається попереднім символом на виході джерела, будуємо нерівномірний код. Застосовуючи методику Хаффмена або Шеннона-Фано, легко отримати коди, що наведені в таблицях.
Після символу А :
Таблиця 7.9
| Символ, що очікується | Умовна ймовірність | Кодова комбінація (КК) | Довжина КК |
| А | p(A/A) = 0,15 | ||
| В | p(B/A) = 0,10 | ||
| С | p(C/A) = 0,75 |
Після символу В :
Таблиця 7.10
| Символ, що очікується | Умовна ймовірність | Кодова комбінація (КК) | Довжина КК |
| А | p(A/B) = 0,85 | ||
| В | p(B/B) = 0,10 | ||
| С | p(C/B) = 0,05 |
Після символу С :
Таблиця 7.11
| Символ, що очікується | Умовна ймовірність | Кодова комбінація (КК) | Довжина КК |
| А | p(A/C) = 0,15 | ||
| В | p(B/C) = 0,70 | ||
| С | p(C/C) = 0,15 |
Знайдемо значення lcep / A середньої довжини кодової комбінації для коду, який застосовується після символу А :
lcep / A = lA/A × p(A/A) + lB /A × p(B/A) + lC /A × p(C/A) =
= 2 ´ 0,15 + 2 ´ 0,10 +1´ 0,75 = 1,25;
тут lA/A , lB/A , lC/A – довжини кодових комбінацій для кодування відповідно символів А, В, С коду, який застосовується після символу А. Аналогічно отримаємо значення lcep / B , lcep / C середніх довжин кодових комбінацій для кодів, що застосовуються після символів В та С відповідно:
lcep / B = 1,15; lcep / C = 1,3.
Середня довжина lcep кодової комбінації при застосуванні марковського алгоритму
lcep = lcep /A × р(А) + lcep /B × р(B) + lcep /C × р(C),
де р(А), р(В), р(С) – безумовні ймовірності появи символів А, В, С на виході джерела.
У задачі 7.2.6 розглянута методика їх отримання. Застосовуючи її, знаходимо
р(А) = 0,361; р(В) = 0,302; р(С) = 0,337.
Тоді
lcep = 1,237.
Ентропія джерела ( див. задачу 7.2.6 )
H = 1,004 біт.
Відносна різниця між lcep та Н становить
[(1,237 – 1,004) / 1,004] ´ 100% = 23,2% .
Закодуємо послідовність символів, наведену в умовах задачі. Таблиці 7.9 – 7.11 дають змогу виконати таке кодування. Виняток становить перший символ, оскільки незрозуміло, який для нього використовувати код. Є декілька шляхів побудови такого коду. Найпростіший – застосування рівномірного коду, наприклад, такого: A – 00; B – 01; C – 10. Більш раціональний – ефективний код, побудований з урахуванням безумовних ймовірностей появи символів. Один із варіантів такого коду A – 0; B – 11; C – 10. Обираючи цей варіант для кодування першого символу та застосовуючи коди таблиць 7.9 – 7.11 для подальших символів, отримаємо
0001011011011101100110101100001011011.
Кодова послідовність має 37 двійкових символів. Відзначимо, що при кодуванні символів джерела рівномірним двійковим кодом ( мінімальна довжина такого коду в даному випадку становить 2 ) довжина кодової послідовності буде дорівнювати 60.
Задачі
7.3.1.Значення ймовірностей pi , з якими дискретне джерело інформації генерує символи алфавіту, для різних варіантів наведені у таблиці 7.3.1. Побудувати нерівномірні ефективні коди за методиками Шеннона-Фано та Хаффмена для кодування символів джерела. Порівняти ефективність кодів.
Таблиця 7.3.1
| № варіанта | p1 | p2 | p3 | p4 | p5 | p6 | p7 | p8 | p9 |
| 0,31 | 0,08 | 0,05 | 0,14 | 0,02 | 0,20 | 0,08 | 0,07 | 0,05 | |
| 0,11 | 0,16 | 0,03 | 0,26 | 0,04 | 0,05 | 0,03 | 0,02 | 0,30 | |
| 0,55 | 0,07 | 0,04 | 0,04 | 0,15 | 0,07 | 0,05 | 0,03 | ||
| 0,08 | 0,05 | 0,11 | 0,07 | 0,33 | 0,24 | 0,04 | 0,04 | 0,04 | |
| 0,22 | 0,18 | 0,04 | 0,06 | 0,03 | 0,04 | 0,06 | 0,29 | 0,08 | |
| 0,07 | 0,41 | 0,13 | 0,09 | 0,06 | 0,11 | 0,05 | 0,04 | 0,04 | |
| 0,35 | 0,15 | 0,06 | 0,02 | 0,03 | 0,08 | 0,02 | 0,07 | 0,22 | |
| 0,18 | 0,05 | 0,27 | 0,29 | 0,02 | 0,03 | 0,05 | 0,11 | ||
| 0,12 | 0,03 | 0,05 | 0,40 | 0,12 | 0,08 | 0,05 | 0,04 | 0,11 | |
| 0,52 | 0,12 | 0,05 | 0,18 | 0,04 | 0,03 | 0,06 | |||
| 0,26 | 0,14 | 0,05 | 0,10 | 0,07 | 0,11 | 0,02 | 0,20 | 0,05 | |
| 0,04 | 0,33 | 0,17 | 0,06 | 0,02 | 0,12 | 0,05 | 0,16 | 0,05 | |
| 0,28 | 0,03 | 0,04 | 0,15 | 0,05 | 0,04 | 0,07 | 0,34 | ||
| 0,07 | 0,15 | 0,06 | 0,39 | 0,05 | 0,14 | 0,08 | 0,03 | 0,03 | |
| 0,45 | 0,15 | 0,03 | 0,07 | 0,08 | 0,02 | 0,06 | 0,09 | 0,05 | |
| 0,09 | 0,44 | 0,18 | 0,09 | 0,03 | 0,05 | 0,02 | 0,02 | 0,08 | |
| 0,06 | 0,05 | 0,15 | 0,04 | 0,14 | 0,08 | 0,03 | 0,20 | 0,25 | |
| 0,22 | 0,05 | 0,16 | 0,05 | 0,05 | 0,03 | 0,02 | 0,34 | 0,08 | |
| 0,33 | 0,24 | 0,05 | 0,08 | 0,06 | 0,12 | 0,05 | 0,07 | ||
| 0,08 | 0,22 | 0,15 | 0,05 | 0,08 | 0,05 | 0,06 | 0,24 | 0,07 |
7.3.2. Алфавіт немарковського дискретного джерела інформації складається з чотирьох символів: {A,B,C,D}.Чисельні значення ймовірностей виникнення символів для різних варіантів наведені у таблиці 7.3.2. Побудувати нерівномірні ефективні коди за методикою Шеннона-Фано або Хаффмена ( за Вашим бажанням ) для кодування поодиноких символів джерела та слів довжиною у два символи. Оцінити та порівняти ефективність отриманих кодів. Побудованими кодами закодувати фрагмент тексту довжиною у 30 символів, що був вироблений джерелом. Фрагменти текстів для різних варіантів наведені у таблиці 7.3.3.
Таблиця 7.3.2
| № варіанта | p(A) | p(B) | p(C) | p(D) | № варіанта | p(A) | p(B) | p(C) | p(D) |
| 0,15 | 0,63 | 0,05 | 0,17 | 0,16 | 0,43 | 0,07 | 0,34 | ||
| 0,33 | 0,10 | 0,12 | 0,45 | 0,05 | 0,33 | 0,32 | 0,30 | ||
| 0,25 | 0,07 | 0,53 | 0,15 | 0,27 | 0,15 | 0,45 | 0,13 | ||
| 0,08 | 0,35 | 0,11 | 0,46 | 0,24 | 0,04 | 0,64 | 0,08 | ||
| 0,32 | 0,38 | 0,24 | 0,06 | 0,14 | 0,16 | 0,29 | 0,41 | ||
| 0,27 | 0,51 | 0,13 | 0,09 | 0,51 | 0,05 | 0,34 | 0,10 | ||
| 0,65 | 0,15 | 0,06 | 0,14 | 0,28 | 0,22 | 0,07 | 0,43 | ||
| 0,18 | 0,05 | 0,27 | 0,50 | 0,12 | 0,35 | 0,11 | 0,42 | ||
| 0,12 | 0,53 | 0,25 | 0,10 | 0,08 | 0,45 | 0,24 | 0,23 | ||
| 0,42 | 0,22 | 0,18 | 0,18 | 0,25 | 0,15 | 0,51 | 0,09 |
Таблиця 7.3.3
| № варіанта | Фрагмент тексту |
| BBDBDABDBACBBDBDBBBABDBBABBBBD | |
| AADABDDCABAADDADDBACDDDDDCADBA | |
| CCCCCABCDACBDCCCCCDCAACCADCDDC | |
| ABDBDDDCDDBDDDDDBDBDCBDCDBCBDB | |
| BCBABBBAACCBCCAAACABBBBABADAAA | |
| CBBABACAABCBCCABDABCBBBABBDBBB | |
| ACBABAAAADDAADBAADAADBAAAAAADA | |
| CDDCDDDDCCCDDDDDCCCCDCDCBCBCDA | |
| BDBBDAABBBBCBDCBBBBBBBACCCBCBC | |
| CACBADBAAAABABABBABCAACCADACBA | |
| BBDBADABCBBBBADADABADBACBBABCA | |
| DBDBCBABCDBDCBDCCCBCBBDBBCBDCC | |
| BACCBCCCCCADBAAABABABACDCBCACC | |
| CCCACBCACCAACACDCCCCCACACACAAC | |
| DDDACDDCDCCCCBDCCDBBCDBADCAABD | |
| AAADAAAAAADAACBCACACCACCAACBAC | |
| DDAACBCABDAAABCDAADDADDDCBABDB | |
| ABBDDDBBDBCDBDDBBDDDBDADBDDDDD | |
| CADDDDCDBBDBADCBDADBBABCBCDBAB | |
| CBCACCADCCCCDCCACCDDDABCCACBAD |
2.3.3. Алфавіт марковського дискретного джерела інформації, що має глибину пам’яті h = 1, складається з трьох символів: {A,B,C}. Чисельні значення умовних ймовірностей виникнення символів для різних варіантів наведені у другому стовпці таблиці 7.3.4. Побудувати нерівномірні ефективні коди за методикою Шеннона-Фано або Хаффмена для кодування поодиноких символів джерела та слів довжиною у два символи. Розробити марковський алгоритм для кодування символів джерела. Оцінити і порівняти ефективність отриманих кодів та марковського алгоритму. Побудованими кодами закодувати фрагмент тексту довжиною у 30 символів, що був вироблений джерелом. Фрагменти текстів для різних варіантів наведені у третьому стовпці таблиці 7.3.4.
Таблиця 7.3.4
| № варіанта | 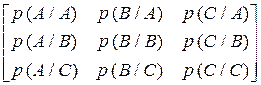
| Фрагмент тексту |
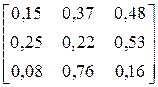
| ACBBABCBBABCCBA BCBCBABCBCACBBC | |
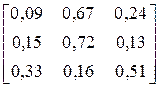
| BCACCCABCCCAACA CCCCABCBBBBBBBA | |
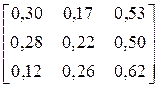
| CCAACCBBCCACCAC CCCBCCCCCBCBCCC | |
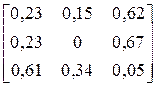
| ACBCACAAAACCACA ACABCCABCACACAA | |
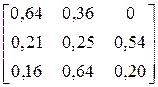
| AABCBAAABBABAAA AAAABBBAAABCBBC | |
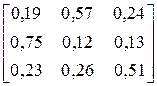
| ABABABACCCCCCAB ABAAAACCCABBACC | |
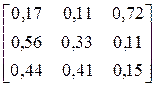
| ACBBBBCBACBACAC ACBACBBACACBACB | |
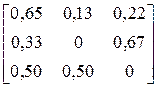
| ACBCBAABAABACAA AAAAABAAACAACBC | |
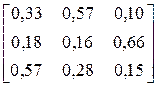
| CBCBCCACAAABBCA ABBCBCAAAACABCB | |
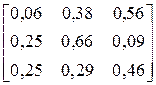
| BABBCACBBACCACC BCABBCCBBBBCACC | |
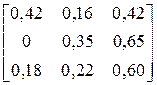
| BCCCCBCCCABCBCB CACCCBCCCCCCCCB | |
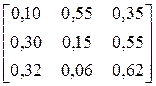
| BCABCABCCABABCC CABABCABCBACAAB | |
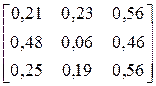
| CCACAACCABCCCAB CAAABCACCBABABA | |
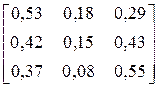
| CABAAAABCAAACAB CBAAACAAAACACCA | |
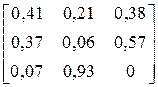
| BACBAAABCBACBCB CBCBAABCBBCBAAB | |
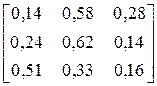
| CABBBBACBCBBBBA BBBABBBABBBABBB | |
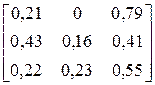
| CACACCCCCBBCCAC CCCCCCCACCBACAA | |
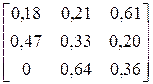
| CCBACBACCBBAACB AACBABAABCBACBA | |
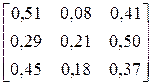
| ACAACCACACCBACA CCBCABACAAACAAC | |
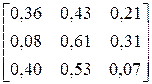
| BCBCBCACBCCBBBB BABBBBBBBBCBBBB |
Дата добавления: 2014-12-22; просмотров: 957;
