Задача 6.2.7

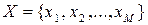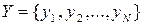Маємо два дискретних джерела з алфавітами та . Перше джерело – марковське з глибиною пам’яті h = 1. Воно описується матрицею умовних ймовірностей

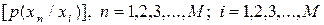
(6.30)

виникнення символу 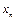при умові, що попереднім був символ 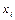. Ймовірність виникнення символу 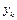на виході другого джерела залежить від того, який символ з’явився на виході першого джерела, тобто ці ймовірності задаються матрицею

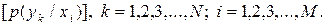
(6.31)

Визначити ентропію другого джерела та повну взаємну інформацію.

Зауважимо, що ця задача моделює ситуацію, коли вихід марковського джерела з глибиною пам’яті 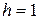подано на вхід стаціонарного дискретного каналу без пам’яті , який задається матрицею перехідних ймовірностей (6.31).

Розв’язання. Друге джерело буде в загальному випадку марковським, більш того, глибина пам’яті цього джерела може перевищувати одиницю. Отримати вираз для ентропії через ймовірності появи символів 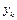на виході другого джерела при цих умовах досить важко, оскільки для цього необхідно знати не тільки безумовні ймовірності 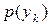, але й умовні – 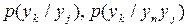тощо. Для вирішення цієї задачі краще скористуватись виразами (1.16, 1.17), з яких можна отримати

.

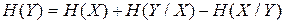(1.32)

Ентропія 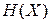для марковського джерела з глибиною пам’яті 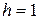знаходиться за виразом (6.27). Розрахунок ентропії для такого джерела при 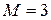наведено в задачі 6.2.6.

Умовна ентропія 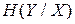знаходиться за виразом (6.7) – значення ймовірностей 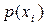та 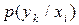є відомими. Щоб визначити умовну ентропію 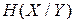, необхідно знати ймовірності 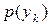та 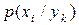. Перші можна отримати таким чином:

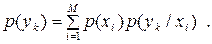
Для ймовірностей 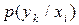маємо із виразу (6.14):

.

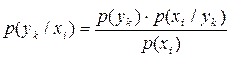Таким чином, отримали всі компоненти, щоб розрахувати всі складові правої частини (6.32).

Припустимо, що перше джерело має характеристики із задачі 6.2.6, потужність алфавіту другого джерела 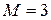, а матриця (6.31) має вигляд

.

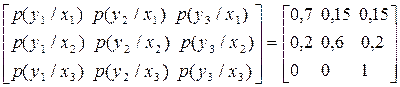Послідовно виконуючи вищезгадані дії, отримаємо:

H(Y/X) = 1,073 біт ;

p(y₁) = 0,56049; p(y₂) = 0,18889; p(y₃) = 0,25062;

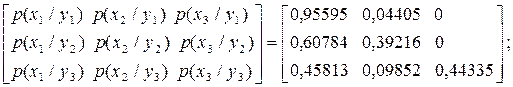
H(X/Y ) = 0,671 біт .

Ураховуючи, що H(X ) = 1,001 біт,маємо H(Y ) = 1,403 біт . Нарешті, повна взаємна інформація

I (X,Y ) = H(X ) – H(X/Y ) = H(Y ) – H(Y/X ) = 0,33 біт .