Задача 6.2.4

Маємо три дискретних немарковських джерела інформації з алфавітами 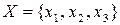, , 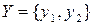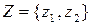. Матриці ймовірностей сумісної появи пар символів є такими:

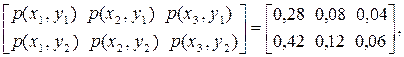
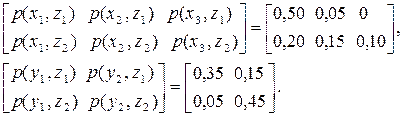
Визначити, між якими джерелами статистичний зв’язок найбільший, а між якими найменший.

Розв’язання.Для відповіді на поставлене запитання треба знайти значення повної взаємної інформації для всіх пар джерел, та порівняти їх. Найпростіше в даному разі користуватись виразом

.

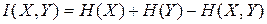Щоб обчислити безумовні ентропії кожного з джерел, знайдемо безумовні ймовірності появи символів на виході джерел за виразом (6.13):

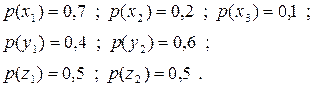
Слід зазначити, що значення кожної з ймовірностей можна отримати двома шляхами. Так 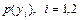є сумою елементів відповідних ря-дків першої матриці, або елементів стовпців третьої матриці. Це означає, що матриці, наведені в завданні, відповідним чином узгоджені.

Розрахуємо ентропії джерел, користуючись (6.1):

H(X) = 1,157 біт ; H(Y) = 0,971 біт ; H(Z) = 1,0 біт .

Далі за виразом (1.11) знаходимо сумісні ентропії:

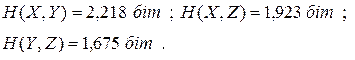
Нарешті отримаємо:

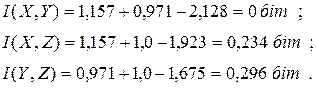
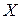Рівність нулю означає, що джерела з алфавітами та 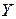статистично незалежні. Найбільший статистичний зв’язок має місце між джерелами з алфавітами 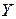та 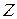,оскільки 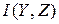має найбільше значення.