Властивості математичного сподівання
1. Математичне сподівання від сталої величини С дорівнює самій сталій:
М (С) = С. (80)
Справді, сталу С можна розглядати як випадкову величину, що з імовірністю, яка дорівнює одиниці, набуває значення С, а тому
М (С) = С × 1 = С.
2.М (СХ) = СМ (Х). (81)
Для дискретної випадкової величини згідно із (75) маємо
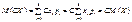 .
.
Для неперервної:
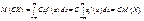
3. Якщо А і В є сталими величинами, то
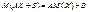 . (82)
. (82)
Для дискретної випадкової величини:
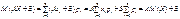 .
.
Для неперервної випадкової величини:
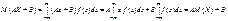
Приклад 1. Закон розподілу дискретної випадкової величини задано таблицею:
| хі | – 6 | – 4 | ||||
| рі | 0,1 | 0,1 | 0,2 | 0,3 | 0,1 | 0,2 |
Обчислити М (Х).Розв’язання. Скориставшись (76), дістанемо
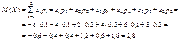 Якщо випадкова величина Х Î [а; b], то М (Х) Î [а; b], а саме: математичне сподівання випадкової величини має обов’язково міститься всередині інтервалу [а; b], являючи собою центр розподілу цієї величини.
Якщо випадкова величина Х Î [а; b], то М (Х) Î [а; b], а саме: математичне сподівання випадкової величини має обов’язково міститься всередині інтервалу [а; b], являючи собою центр розподілу цієї величини.
25. Мода та медіана випадкової величиниМодою (Мo) дискретної випадкової величини Х називають те її можливе значення, якому відповідає найбільша ймовірність появи.Модою для неперервної випадкової величини Х називають те її можливе значення, якому відповідає максимальне значення щільності ймовірності:f (Mо) = max.Якщо випадкова величина має одну моду, то такий розподіл імовірностей називають одномодальним; якщо розподіл має дві моди — двомодальним і т. ін. Існують і такі розподіли, які не мають моди. Їх називають антимодальними.Медіаною (Ме) неперервної випадкової величини Х називають те її значення, для якого виконуються рівність імовірностей подій: 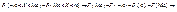
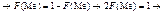
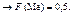 (83)Отже, медіану визначають із рівняння (83).Приклад 5. Робітник під час роботи обслуговує три верстати-автомати. Імовірність того, що верстат-автомат потребує уваги робітника за певний проміжок часу, — величина стала і дорівнює 0,8.Побудувати закон розподілу ймовірностей дискретної випадкової величини Х — числа верстатів, які потребують уваги робітника за певний проміжок часу. Знайти Мо.Розв’язання. Можливі значення випадкової величини:Х = 0, 1, 2, 3.Імовірності цих можливих значень такі:p1 = (0,2)3 = 0,008;p2 = 3р q2 = 3 × 0,8 × 0,04 = 0,096;p3 = 3p2q = 3 × 0,64 × 0,2 = 0,384;p4 = p3 = (0,8)3 = 0,512.Запишемо закон таблицею:
(83)Отже, медіану визначають із рівняння (83).Приклад 5. Робітник під час роботи обслуговує три верстати-автомати. Імовірність того, що верстат-автомат потребує уваги робітника за певний проміжок часу, — величина стала і дорівнює 0,8.Побудувати закон розподілу ймовірностей дискретної випадкової величини Х — числа верстатів, які потребують уваги робітника за певний проміжок часу. Знайти Мо.Розв’язання. Можливі значення випадкової величини:Х = 0, 1, 2, 3.Імовірності цих можливих значень такі:p1 = (0,2)3 = 0,008;p2 = 3р q2 = 3 × 0,8 × 0,04 = 0,096;p3 = 3p2q = 3 × 0,64 × 0,2 = 0,384;p4 = p3 = (0,8)3 = 0,512.Запишемо закон таблицею:
| хі | ||||
| рі | 0,008 | 0,096 | 0,384 | 0,512 |
Із таблиці визначаємо Мo = 3.Отже, дістаємо одномодальний розподіл.Ме— можливе значення випадкової величини Х, причому таке, що пряма, проведена перпендикулярно до відповідної точки на площині Х = Ме, поділяє площу фігури, яка обмежена функцією f (x), на дві рівні частини.
Дата добавления: 2014-11-29; просмотров: 1323;
