Біноміальний закон розподілу ймовірностей

Цілочислова випадкова величина X має біноміальний закон розподілу, якщо ймовірність її можливих значень обчислюється за формулою Бернуллі:

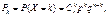k = 0, 1, 2, 3, ..., n.(234 а)

У табличній формі цей закон набирає такого вигляду:

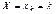
					...	n

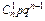
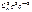
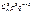
При перевірці виконання умови нормування використовується фор­мула біному Ньютона, тому закон розподілу називають біноміальним:

.

Побудуємо ймовірнісну твірну функцію для цього закону

.

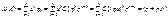Отже, імовірнісна твірна функція для біноміального закону

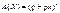. (234 b)

Знайдемо основні числові характеристики для цього закону:

1.

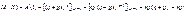
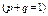
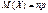. (235)

2. ; ;

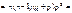
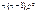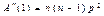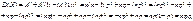
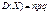; (236)

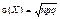. (237)

Приклад 1. У партії однотипних деталей стандартні становлять 95%. Навмання з партії беруть 400 деталей. Визначити
М (Х), D (X), s (Х) для дискретної випадкової величини Х — появи числа стандартних деталей серед 400 навмання взятих.Розв’язання.Цілочислова випадкова величина Х має біноміальний закон розподілу ймовірностей, яка може набувати значення Х = k = 0, 1, 2, ..., 400.Імовірності можливих значень обчислюються за формулою Бернуллі: 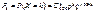, де р = 0,95 — імовірність появи стандартної деталі, q = 1 – p =1 – 0,95 = 0,05 — імовірність появи нестандартної деталі.Згідно з (235), (236), (237), маємо:

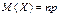= 400 × 0,95 = 380;

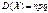= 400 × 0,95 × 0,05 = 19;

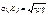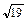= » 4,36.