Нормальний закон розподілу

Випадкова величина Х має нормальний закон розподілу ймо­вірностей, якщо

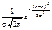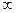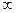f (х) = , – < x < , (257)

де а = М (X), s = s (X). Отже, нормальний закон визначається звідси параметрами а і s і називається загальним.

Тоді

F(x)= 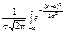dx. (258)

Якщо а = 0 і s = 1, то нормальний закон називають нормованим.

У цьому разі

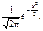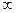f (x)= – < x < 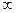, (259)

тобто f (x) = j(x) є функцією Гаусса,

F(x) = 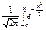dx. (260)

Графіки f (x), F(x) для загального нормального закону залежно від параметрів а і s зображені на рис. 91 і 92.

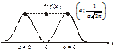
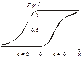
Рис. 91 Рис. 92

Із рис. 91 бачимо, що графік f (x) розміщений симетрично відносно умовно проведеного перпендикуляра в точку Х = а. Зі зміною значень параметра а крива f (x) зміщується праворуч, якщо а > 0 або ліворуч, якщо a < 0, не змінюючи при цьому своєї форми; f (a) = max, отже, Мо= а.

Із рис. 92 бачимо, що графік F(x) є неспадною функцією, оскільки f (x) = F¢(x) > 0 і, як буде доведено далі, F(a) = 0,5.

Отже, Ме = а.

Зі зміною значень параметра а крива F(x) зміщується праворуч для а > 0 або ліворуч при а < 0, не змінюючи при цьому форми кривої.

Отже, для нормального закону Мо = Ме = а.

Зі зміною значень s при а = const змінюється крутизна кривих у околі значень X = а, що унаочнюють рис. 93 і 94.

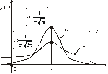
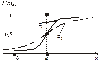
Рис. 93 Рис. 94

Для нормованого нормального закону графіки функцій f (x), F (x) зображено на рис. 95 і 96.

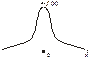
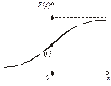
Рис. 95 Рис. 96

Загальний нормальний закон позначають: N (a; s). Так, наприк­лад, N (–2; 4) — загальний нормальний закон із значенням параметрів а = –2, s = 4.

Нормований нормальний закон позначають N (0; 1).

44.Правило трьох сигм
для нормального закону

Коли 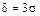, то згідно з (262) маємо:

.

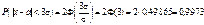Практично ця подія при одному експерименті здійсниться, а тому її вважають практично вірогідною. Звідси:

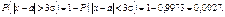
Тобто ймовірність того, що внаслідок проведення експерименту випадкова величина Х, яка має закон розподілу N (a; s), не потрапить у проміжок 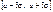, дорівнює 0,0027. Це становить 0,27%, тобто практично вважається, що ця подія внаслідок прове­дення одного експерименту не здійсниться.

46.. Розподіл c²(хі-квадрат)

Нормальному закону розподілу належить центральне місце в побудові статистичних моделей у теорії надійності та математичній статистиці.

Якщо кожна із X_і (і = 1, 2, …, k) незалежних випадкових величин характеризується нормованим законом розподілу ймовірностей 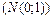, то випадкова величина 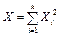матиме розподіл c² із k ступенями свободи, щільність імовірностей якої буде

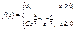
Використовуючи умову нормування, знаходимо

;

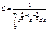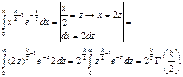
Тоді 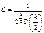(304)

Отже, 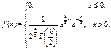(305)

Функція розподілу ймовірностей 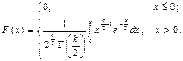(306)