Лінійна множинна регресія.
Визначення статистичних точкових оцінок
Розглянемо лінійну залежність 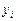 від m аргументів
від m аргументів 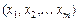 .
.
Лінійна модель у цьому разі набирає такого вигляду
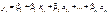 . (541)
. (541)
Для вибірки обсягу n матимемо систему лінійних рівнянь
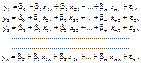 (542)
(542)
де 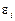 — випадкова величина, що має нормальний закон розподілу з числовими характеристиками
— випадкова величина, що має нормальний закон розподілу з числовими характеристиками 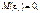
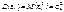 і при цьому
і при цьому 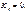 У векторно-матричній формі система (542) набирає такого вигляду:
У векторно-матричній формі система (542) набирає такого вигляду:
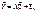 (543)
(543)
де
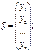
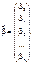
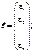
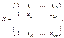
Матрицю Х розміром 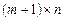 називають регресійною, а елементи
називають регресійною, а елементи 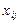 цієї матриці — регресорами. Параметри рівняння (541) є величинами сталими, але невідомими. Ці параметри оцінювання статистичними точковими оцінками
цієї матриці — регресорами. Параметри рівняння (541) є величинами сталими, але невідомими. Ці параметри оцінювання статистичними точковими оцінками 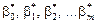 , які дістають шляхом обробки результатів вибірки, і є величинами випадковими. Таким чином, рівнянню (541) відповідає статистична оцінка
, які дістають шляхом обробки результатів вибірки, і є величинами випадковими. Таким чином, рівнянню (541) відповідає статистична оцінка
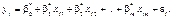 (544)
(544)
Статистична оцінка для вектора 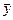 буде визначатись вектором
буде визначатись вектором
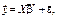 (545)
(545)
де
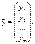
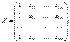
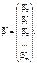
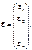
Вектор похибок дорівнюватиме
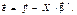 (546)
(546)
Для визначення компонентів вектора 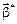 (статистичних точкових оцінок компонентів вектора
(статистичних точкових оцінок компонентів вектора 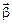 ) застосовується метод найменших квадратів.
) застосовується метод найменших квадратів.
Знайдемо суму квадратів усіх похибок:
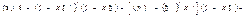
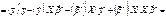
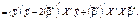
Тут застосовано такі рівності: 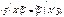
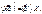
Мінімізуючий добуток 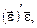 а саме:
а саме:
прирівнюючи частинні похідні за елементами вектора 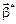 до нуля, дістаємо:
до нуля, дістаємо:
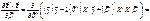
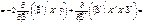
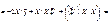
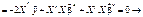
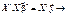
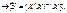 (547)
(547)
Довірчий інтервал для множинної лінійної регресії
Матриця Х містить m лінійно незалежних векторів-стовпців, а це означає, що ранг її дорівнюватиме m і визначник 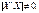 Отже, матриця
Отже, матриця 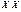 має обернену.
має обернену.
Дисперсії статистичних оцінок 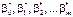 визначають з допомогою кореляційної матриці для вектора
визначають з допомогою кореляційної матриці для вектора 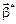 .
.
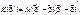
Оскільки 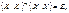 то, скориставшись (545), (547), дістанемо
то, скориставшись (545), (547), дістанемо
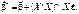 (548)
(548)
Тоді маємо
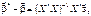 (549)
(549)
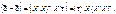 (550)
(550)
Скориставшись (549), (550), дістанемо
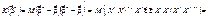
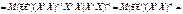
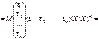
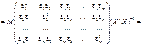
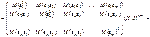
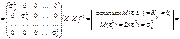
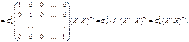
Таким чином, маємо
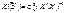 . (551)
. (551)
Оскільки 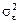 є невідомою величиною, то в (551) замість
є невідомою величиною, то в (551) замість 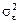 підставляють його точкову незміщену статистичну оцінку за аналогією з (513).
підставляють його точкову незміщену статистичну оцінку за аналогією з (513).
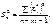 (552)
(552)
де n є кількістю спостережень, а m — кількістю оцінюваних параметрів множинної лінійної регресії.
Значення дисперсії для 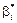
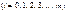 обчислюють за формулою
обчислюють за формулою
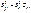 (553)
(553)
де 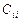 — діагональний елемент матриці
— діагональний елемент матриці 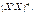
Розглянемо рівняння лінійної множинної регресії з параметрами 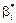
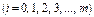 , знайденими за результатами вибірки
, знайденими за результатами вибірки
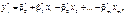
де 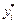 — лише одне з можливих значень прогнозної величини для заданих значень
— лише одне з можливих значень прогнозної величини для заданих значень 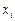 .
.
Ураховуючи те, що 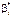
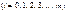 є випадковими величинами, то
є випадковими величинами, то 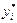 буде також випадковою, а тому матиме дисперсію.
буде також випадковою, а тому матиме дисперсію.
Отже,
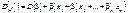
Використовуючи властивості дисперсії від суми залежних випадкових величин (випадкові величини 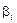 є залежними), дістанемо:
є залежними), дістанемо:
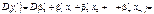
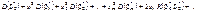
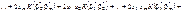
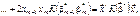
оскільки це є квадратична форма, яку можна записати у векторно-матричній формі.
Отже, маємо
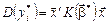 . (554)
. (554)
Тоді, використовуючи (551), дістанемо
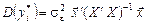 . (555)
. (555)
Оскільки 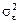 — невідома величина, то в (555) використовуємо її точкову незміщену статистичну оцінку
— невідома величина, то в (555) використовуємо її точкову незміщену статистичну оцінку 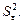
Таким чином, маємо:
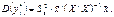 (556)
(556)
Отже, істинне значення Y перебуватиме в інтервалі:
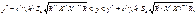 (557)
(557)
який називають довірчим.
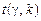 є випадковою величиною, що має розподіл Стьюдента з
є випадковою величиною, що має розподіл Стьюдента з 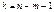 ступенями свободи і обчислюється за таблицею (додаток 7) за заданою надійністю γ та числом ступенів свободи k.
ступенями свободи і обчислюється за таблицею (додаток 7) за заданою надійністю γ та числом ступенів свободи k.
Якщо до значень 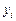 — прогнозне значення — додати можливі відхилення ознаки Y від функції регресії, то до дисперсії
— прогнозне значення — додати можливі відхилення ознаки Y від функції регресії, то до дисперсії 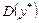 необхідно додати дисперсію випадкової величини
необхідно додати дисперсію випадкової величини 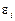 —
— 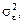 тобто його точкову незміщену статистичну оцінку
тобто його точкову незміщену статистичну оцінку 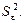
У цьому разі
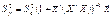 . (558)
. (558)
І довірчий інтервал тепер дорівнюватиме:
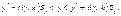 (559)
(559)
Коефіцієнт множинної регресії
Тісноту між ознаками Y та X, де 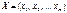 , вимірюють з допомогою коефіцієнта множинної кореляції R, що є узагальненням парного коефіцієнта кореляції rij і обчислюється за формулою
, вимірюють з допомогою коефіцієнта множинної кореляції R, що є узагальненням парного коефіцієнта кореляції rij і обчислюється за формулою
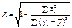 . (560)
. (560)
Чим ближче значення R до ±1, тим краще вибрано функцію регресії
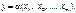
Оскільки 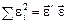 , то
, то
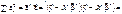
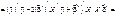
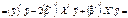
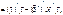
оскільки 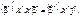
При цьому 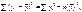 а оскільки
а оскільки 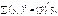 то остаточно маємо
то остаточно маємо
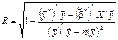 . (561)
. (561)
Нормування коефіцієнтів регресії
Множинна лінійна регресія дає змогу порівняти вплив на досліджуваний процес різних чинників. У загальному випадку змінні 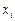 репрезентують чинники, що мають різні одиниці виміру (кілограми, гривні, метри тощо). Отже, для того щоб порівняти і з’ясувати відносну вагомість кожного з чинників, використовують так звані нормовані коефіцієнти регресії, які визначають за формулою
репрезентують чинники, що мають різні одиниці виміру (кілограми, гривні, метри тощо). Отже, для того щоб порівняти і з’ясувати відносну вагомість кожного з чинників, використовують так звані нормовані коефіцієнти регресії, які визначають за формулою
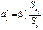
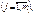 (562)
(562)
де 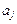 — коефіцієнт регресії після нормування;
— коефіцієнт регресії після нормування; 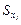 — виправлене середнє квадратичне відхилення змінної
— виправлене середнє квадратичне відхилення змінної 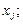
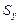 — виправлене середнє квадратичне відхилення ознаки Y.
— виправлене середнє квадратичне відхилення ознаки Y.
Приклад 1. Ознака Y — лінійно залежна від 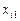 ,
, 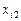 ,
, 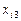 . Результати спостережень наведено в таблиці:
. Результати спостережень наведено в таблиці:
| i | уі | хі1 | хі2 | хі3 |
Необхідно:
1) знайти компоненти вектора і побудувати лінійну
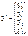
функцію регресії 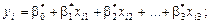
2) обчислити R;
3) побудувати довірчий інтервал із надійністю 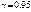 для множинної лінійної функції регресії та визначити дисперсії для
для множинної лінійної функції регресії та визначити дисперсії для 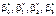 і оцінити ефективність впливу на ознаку Y незалежних змінних
і оцінити ефективність впливу на ознаку Y незалежних змінних 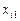 ,
, 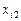 ,
, 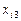 .
.
Розв’язання. 1. З умови задачі маємо:
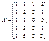
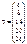
Оскільки
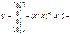
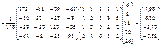
Отже, дістали: 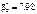
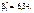
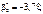
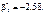
Рівнянням регресії буде
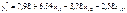
2. Знайдемо R. Для цього необхідно визначити
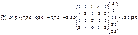
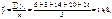
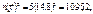
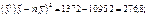
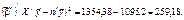
Тоді
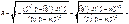
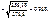
Для побудови довірчого інтервалу для множинної лінійної функції регресії необхідно обчислити 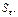 Оскільки
Оскільки 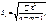 то в цьому разі результати обчислень зручно подати у вигляді таблиці:
то в цьому разі результати обчислень зручно подати у вигляді таблиці:
| i | 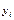
| 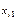
| 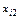
| 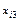
| 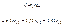
| 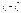
| 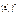
|
| 5,38 | 0,62 | 0,3844 | |||||
| 10,52 | –2,52 | 6,3504 | |||||
| 14,32 | –0,32 | 0,1024 | |||||
| 16,86 | 3,14 | 9,8596 | |||||
| 26,96 | –0,96 | 0,9216 | |||||
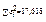
|
Таким чином, дістанемо:
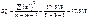
Візьмемо 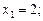
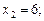
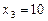 і обчислимо
і обчислимо
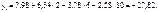
Знайдемо
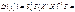
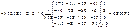
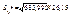
Для побудови довірчого інтервалу знаходимо
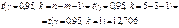
Тоді 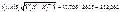
І довірчий інтервал дорівнюватиме
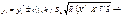
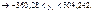
Оскільки діагональні елементи матриці 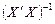 відповідно дорівнюють
відповідно дорівнюють
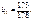
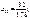
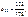
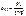
то відповідно дістанемо
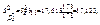
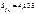
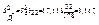
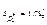
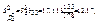
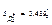
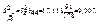
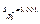
Обчислимо
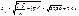
Визначимо нормовані коефіцієнти регресії:
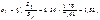
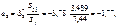
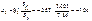
Отже, для змінної 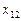 вплив на ознаку Y є найефективнішим порівняно з дією змінних
вплив на ознаку Y є найефективнішим порівняно з дією змінних 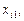
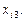
Дата добавления: 2014-11-29; просмотров: 2045;
