Геометричний закон розподілу ймовірностей
Інколи спроби здійснюють до першої появи випадкової події. Число проведених спроб буде цілочисловою випадковою величиною. Цілочислова випадкова величина Х має геометричний закон розподілу, якщо ймовірності її можливих значень
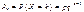 , k = 1, 2, 3, …, n.(243)
, k = 1, 2, 3, …, n.(243)
Тут p — імовірність появи випадкової події в кожній спробі — є величиною сталою, q = 1 – p.
У табличній формі геометричний закон розподілу такий:
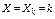
| ... | ||||
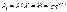
| 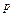
| 
| 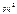
| 
| ... |
При перевірці умови нормування використовується формула суми нескінченної геометричної прогресії, тому й закон розподілу називають геометричним:
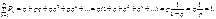
Побудуємо ймовірнісну твірну функцію
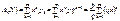 .
.
Ураховуючи, що 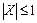 , дістаємо
, дістаємо
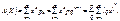
Оскільки 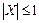 , то
, то
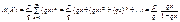 ;
;
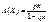 . (244)
. (244)
Числові характеристики для цього закону:
1. 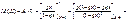
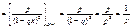 ;
;
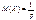 . (245)
. (245)
2. 
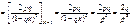 ;
;
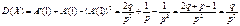 .
.
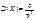 ; (246)
; (246)
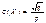 . (247)
. (247)
Серед дискретних випадкових величин лише геометричному закону притаманна властивість відсутності післядії. Це означає, що ймовірність появи випадкової події в k-му експерименті не залежить від того, скільки їх з’явилося до k-го, і завжди дорівнює p.
Приклад 5. Гральний кубик підкидається до першої появи цифри 6. Визначити М (Х), D (X), s (Х) для випадкової величини Х числа здійснюваних підкидань.
Розв’язання. Випадкова величина Х є цілочисловою, що має геометричний закон розподілу ймовірностей. За умовою задачі: p = 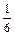 ; q =
; q = 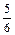 .
.
Скориставшись (245), (246), (247), дістанемо:
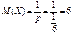 ;
; 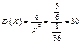 ;
; 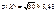 .
.
Дата добавления: 2014-11-29; просмотров: 1449;
