Функції одного випадкового аргументу

Функцією випадкового аргументу Х називають таку випадкову величину Y, яка набуває значення Y = у = 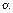(х) щоразу, коли Х = х, де 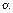є невипадковою функцією. Якщо Х є дискретною випадковою величиною, то і функція випадкового аргументу Y = 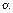(х) буде дискретною.

Коли Х є неперервною випадковою величиною, то і Y = 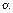(х) буде неперервною.

Нехай закон дискретної випадкової величини Х задано таблицею:

Х = х_i	x₁	x₂	x₃	.....	x_k
P(X = x_i) = p_i	p₁	p₂	p₃	.....	p_k

Тоді закон розподілу випадкової величини Y = 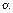(х) матиме такий вигляд:

Y = α (х_i)	α (х₁)	α (х₂)	α (х₃)	.	α (х_k)
P(Y = α (х_i) = р_i	p₁	p₂	p₃	...	p_k

де кожне можливе значення Y дістають, виконуючи ті операції, які вказані в невипадковій функції, умовно позначеній α.

При цьому, якщо в законі розподілу випадкової величини Y є повторення значень, то кожне з цих значень записують один раз, додаючи їх імовірності.

Приклад 1.

Закон розподілу дискретної випадкової величини Х задано таблицею:

Х = х_i	– 4	–2	–1
Р(X = х_i) = р_i	0,1	0,2	0,1	0,1	0,2	0,3

Побудувати закон розподілу ймовірностей для Y = 3х².

Розв’язання. Iз функціональної залежності Y = 3х² маємо:

Y = 3х_i²
Р(у = 3х_i²) = р_i	0,1	0,2	0,1	0,1	0,2	0,3

Ураховуючи повтори можливих значень Y, дістаємо:

Р (у = 16) = 0,1 + 0,3 = 0,4;

Р (у = 4) = 0,2 + 0,2 = 0,4;

Р (у = 1) = 0,1 + 0,1 = 0,2.

Отже, закон розподілу дискретної випадкової величини Y набирає такого вигляду:

Y = у_j
Р (у = у_j) = р_j	0,2	0,4	0,4

<15 16 171819 20 21 >

Дата добавления: 2014-11-29; просмотров: 1579;