Амплитудно-фазовая характеристика АФХ отражает как свойство изменять амплитуду выходного сигнала, так и свойство задерживать сигнал на каждой частоте на определенную величину j.

Выражение для построения АФХ получают из передаточной функции W(p) заменой комплексной переменной р на jw.

Так как W(jw) комплексная функция, то её можно представить в алгебраической и показательной форме записи.

Алгебраическая форма записи:

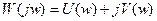
Здесь U(w)-вещественная частотная характеристика (ВЧХ);

V(w)-мнимая частотная характеристика (МЧХ).

Показательная форма записи связывает АФХ с АЧХ и ФЧХ:

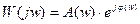
Амплитудно-фазовую характеристику строят на комплексной плоскости (рис. 3.3.3).

JV(w)

j(w0)

U(w)

A(w0)

w0

Рис. 3.3.3 Пример АФХ

АЧХ является модулем АФХ:

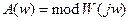
Длина вектора, проведённого из начала координат в точку характеристики W(jw0),равна значению АЧХ на частоте w0.

ФЧХ является аргументом АФХ:

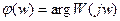
Величина угла от оси абсцисс до вектора, проведённого из начала координат в точку характеристики W(jw0), равна значению ФЧХ на частоте w0.