Типовые звенья САР и их характеристики

Типовые динамические звенья делятся на позиционные, интегрирующие, дифференцирующие и запаздывания в соответствии со структурой их уравнений.

1. Позиционные звеньяв правой части уравнения содержат только входную величину, в левой- выходную величину и её производные. К позиционным звеньям относятся:

Усилительное звено, апериодическое звено 1-го порядка, апериодическое звено 2-го порядка, колебательное звено, консервативное звено.

Динамика работы усилительного звена описывается алгебраическим уравнением:

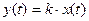и передаточной функцией:

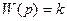
Апериодическое звено 1-го порядка описывается дифференциальным уравнением:

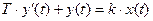и передаточной функцией:

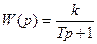, где к- коэффициент передачи, Т- постоянная времени звена,с.

Апериодическое звено 2-го порядка описывается дифференциальным уравнением:

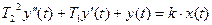и передаточной функцией:

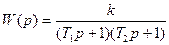
к – коэффициент передачи; 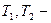постоянные времени,с.

Колебательное звено описывается дифференциальным уравнением:

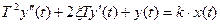и передаточной функцией:

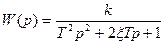
x-параметр затухания.

Консервативное звено описывается дифференциальным уравнением вида:

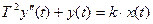и передаточной функцией:

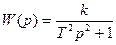
Все позиционные звенья являются статическими, то есть при подаче на вход единичного ступенчатого воздействия, выходная величина стремится к новому установившемуся значению.

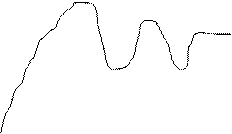
На рисунке 3.4.1 приведены переходные характеристики позиционных звеньев.

h(t) 4

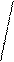
1 2 5

3

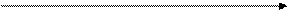t

Рис. 3.4.1 Переходные характеристики позиционных

звеньев

1-усилительное звено;

2-апериодическое звено 1-го порядка;

3-апериодическое звено 2-го порядка;

4-колебательное звено;

5-консервативное звено.

2. К интегрирующим относятся звенья, выходной сигнал которых получается интегрированием входного сигнала.

Идеальное интегрирующее звено описывается уравнением:

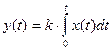или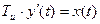

где 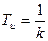- постоянная интегрирования.

Передаточная функция звена:

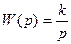
Инерционное интегрирующее звено описывается уравнением:

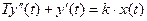
Передаточная функция звена:

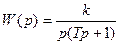
Инерционное интегрирующее звено можно представить как последовательное соединение идеального интегрирующего звена и апериодического звена 1-го порядка.

Изодромное звено описывается уравнением:

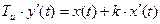
Передаточная функция звена:

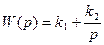
Изодромное звено можно представить как параллельное соединение усилительного и идеального интегрирующего звена.

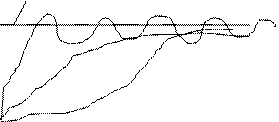
Интегрирующие звенья являются астатическими, то есть при подаче на вход единичного ступенчатого воздействия выходная величина бесконечно возрастает, не достигая нового установившегося значения. На рис.3.4.2 представлены переходные характеристики интегрирующих звеньев.

h 3

2

k1 1

t

Рис.3.4.2 Переходные характеристики интегрирующих звеньев.

1-идеальное интегрирующее звено; 2-инерционное интегрирующее звено; 3-изодромное звено.

3.У дифференцирующих звеньев выходная величина получается дифференцированием входного сигнала.

Идеальное дифференцирующее звено описывается уравнением:

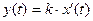
Передаточная функция звена:

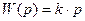
Инерционное дифференцирующее звено описывается уравнением:

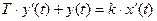
Передаточная функция звена:

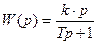
Инерционное дифференцирующее звено можно представить в виде последовательного соединения идеального дифференцирующего звена и апериодического звена 1-го порядка.

При подаче на вход дифференцирующих звеньев единичного входного воздействия на выходе сначала появляется сигнал бесконечно большой амплитуды, затем его величина падает до нуля.

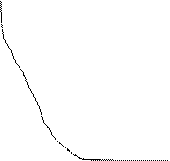
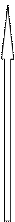На рис. 3.4.3 приведены переходные характеристики дифференцирующих звеньев.

1

h

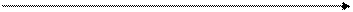
2 t

Рис.3.4.3 Переходные характеристики дифференцирующих звеньев

1- идеальное дифференцирующее звено;

2- инерционное дифференцирующее звен

Запаздывающее звено передаёт входной сигнал без искажения его формы, однако осуществляет задержку на время 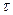, то есть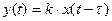

Передаточная функция звена:

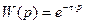
x(t) y(t)

k×x(t-t)

1 1(t)

t t

t

а) входной сигнал б)выходной сигнал

Рис.3.4.4 Примеры входного и выходного сигналов звена запаздывания