Розв’язання. Скориставшись умовою нормування (108), дістанемо:
Скориставшись умовою нормування (108), дістанемо:
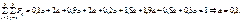
Зі знайденим а закон системи набирає такого вигляду:
 Х = хj
Y = yi Х = хj
Y = yi
| 5,2 | 10,2 | 15,2 | Pyi |
| 2,4 | 0,01 | 0,2 | 0,09 | 0,3 |
| 4,4 | 0,2 | 0,02 | 0,18 | 0,4 |
| 6,4 | 0,19 | 0,08 | 0,03 | 0,3 |
| Pxj | 0,4 | 0,3 | 0,3 |
Основні числові характеристики обчислюємо за формулами (109) — (116):
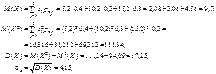
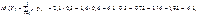
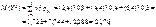

Оскільки Κху > 0, то між відповідними величинами існує кореляційний зв’язок. Для вимірювання тісноти кореляційного зв’язку обчислимо коефіцієнт кореляції

33. Функція розподілу ймовірностей системи двох випадкових величин та її властивості
Функцією розподілу ймовірностей системи двох випадкових величин (Х, Y) називають таку функцію двох аргументів х, у, яка визначає ймовірність cпільної появи подій (X < x) I (Y < y):
F(x,y) = P((X < x) I (Y < y)). (123)
Геометрично ця функція зображена на рис. 62

Рис. 62
Властивості F(x, y)
1. 0 £ F(x, y) £ 1, оскільки 0 £ P((X < x) I (y < y)) £ 1.
2. Якщо один із аргументів F(x, y) прямує до + 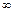 , то функція розподілу системи прямує до функції розподілу одного аргументу, що не прямує до +
, то функція розподілу системи прямує до функції розподілу одного аргументу, що не прямує до + 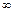 , а саме:
, а саме:
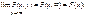 (124)
(124)
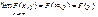 (125)
(125)
3. 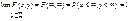 . (126)
. (126)
4. 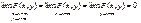 (127)
(127)
5. F(x, y) є неспадною функцією аргументів х і у.
6. Імовірність влучення точки (Х, Y) в довільний прямокутник
(a < X< b, c < Y < d) обчислюємо так:
P(a < x < b, c < y < d) = F(b, d) + F(a, c) – F(a, d) – F(b, c). (129)
Приклад 4. Закон розподілу системи двох неперервних випадкових величин (Х, Y) задано функцією розподілу ймовірностей
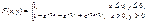
Обчислити P(0 < x < 4,0 < y < 2).
Розв’язання. Відповідну графічну схему зображено на рис. 65.

Рис. 65
Далі згідно зі (129) маємо:
P(0 < x < 4; 0 < y < 2) = F(4; 2) + F(0; 0) – F(0; 2) – F(4; 0) = 1 – e – 8 – e – 6 + e – 14.
34. Щільність імовірностей системи двох неперервних випадкових величин (Х, Y), f(x, y) та її властивості
Характеристикою системи неперервних випадкових величин є щільність імовірностей.
Для визначення щільності ймовірностей системи двох неперервних випадкових величин (Х, Y) застосовується формула (129).
Розглянемо прямокутник зі сторонами Dх та Dу (рис. 66).

Рис. 66
Імовірність розміщення системи (Х, Y) у прямокутній області
(x < X < x + Dx, y < Y < y + Dy) обчислюється за формулою
P(x < X < x + Dx, y < Y < y + Dy) = F(x + Dx, y + Dy) + F(x, y) – F(x + Dx, y) – F(x, y + Dy).
Поділивши цю ймовірність на площу прямокутника Dx, Dy і спрямувавши Dx ® 0, Dy ® 0, дістанемо ймовірність у точці, тобто щільність:

Отже,
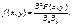 (130)
(130)
Функція f (x, y) може існувати лише за умови, що F (x, y) є неперервною за аргументами х і у та двічі диференційовною.
Функції f (x, y) у тривимірному просторі відповідає певна поверхня — так звана поверхня розподілу ймовірностей системи двох неперервних випадкових величин (Х, Y).
Тоді f (x, y) dxdy — імовірність розміщення системи двох випадкових величин у прямокутнику зі сторонами dx, dy.
Властивості f (x, y)
1. Функція f (x, y) ³ 0, оскільки F(x, y) є неспадною відносно аргументів х і у.
2. Умова нормування системи двох неперервних випадкових величин (Х, Y) така:
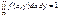 (131)
(131)
Якщо 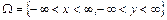 , то (131) набирає такого вигляду:
, то (131) набирає такого вигляду:
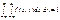 . (132)
. (132)
3. Імовірність розміщення системи змінних (х, у) в області  обчислюється так:
обчислюється так:
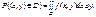 (133)
(133)
Імовірність розміщення системи змінних (х, у) у прямокутній області D = (a < x < b, c < y < d)
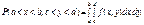 (134)
(134)
4. Функція розподілу ймовірностей системи двох змінних визначається з рівняння
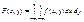 (135)
(135)
5. Якщо  , то
, то 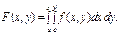 (136)
(136)
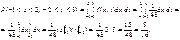
35. Основні числові характеристики для системи двох неперервних випадкових величин (Х, Y)  (137)
(137)
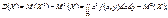 (138)
(138)
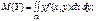 (139)
(139)
 (140)
(140)
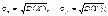 (141)
(141)
 (142)
(142)
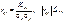
Якщо 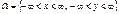 , то виконуються співвідношення:
, то виконуються співвідношення:
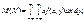 (143)
(143)
 (144)
(144)
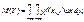 (145)
(145)
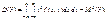 (146)
(146)
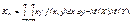 (147)
(147)
Якщо 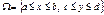 , то маємо:
, то маємо:
 (148)
(148)
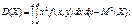 (149)
(149)
 (150)
(150)
 (151)
(151)
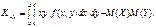 (152)
(152)
Дата добавления: 2014-11-29; просмотров: 1217;
