Математичне сподівання Функції одного випадкового аргументу
1. Математичне сподівання 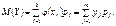 (190)
(190)
2. Дисперсія 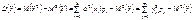 . (191)
. (191)
3. Середнє квадратичне відхилення 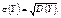 (192)
(192)
Приклад 2. За заданим законом розподілу
Обчислити  М (Y), D (Y), s (Y), якщо Y = cos2 х.
М (Y), D (Y), s (Y), якщо Y = cos2 х.
Розв’язання. Побудуємо закон розподілу Y.
| Y = cos2 хi | 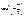
| 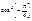
| 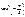
| 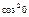
| 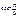
| 
| 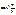
|
| Р (Y = cos2 хi) = pi | 0,1 | 0,2 | 0,1 | 0,1 | 0,2 | 0,1 | 0,2 |
або
| Y = cos2 хi | 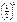
| 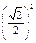
| 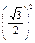
| 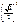
| 
| 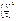
| ||
| Р (Y = cos2 хi) = pi | 0,1 | 0,2 | 0,1 | 0,1 | 0,2 | 0,1 | 0,2 | |
| Y = cos2 хi | 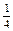
| 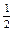
| 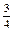
| 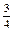
| 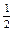
| 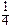
| |
| Р (Y = cos2 хi) = pi | 0,1 | 0,2 | 0,1 | 0,1 | 0,2 | 0,1 | 0,2 |
| Y = уj | 0,25 | 0,5 | 0,75 | |
| Р (Y = уj) = pj | 0,3 | 0,3 | 0,3 | 0,1 |
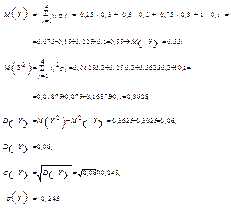
39.Функції двох випадкових аргументів
та їх числові характеристики
У загальному випадку функцію двох аргументів Х і Y можна позначити як
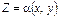 , (202)
, (202)
де 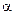 є невипадковою функцією.
є невипадковою функцією.
Якщо Х та Y є дискретними випадковими величинами, то і Z буде дискретною. Якщо Х та Y є неперервними, то і Z буде неперервною.
4.1. Знаходження F (z), f (z), якщо Z = Х + Y
Розглянемо функціональну залежність Z = Х + Y, де Х і Y є неперервними випадковими величинами.
Потрібно за відомою щільністю f (x, y) знайти F (z), f (z).
Імовірність влучення Z в області Z < z, а саме Z < Х + Y зображено на рис. 76.

Рис. 76
Ця ймовірність обчислюється так:
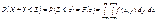 (203)
(203)
або
(204)
Оскільки 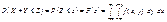
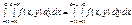 ,
,
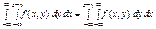 ,
,
то формули (203), (204) можна подати так:
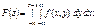 (205)
(205)
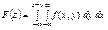 (206)
(206)
Тоді щільність імовірностей для випадкової величини Z буде така:
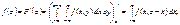
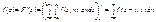
Отже,
 (207)
(207)
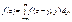 (208)
(208)
Якщо випадкові величини Х і Y є незалежними, то f (x, y) =
= f (x) f (y). За цієї умови формули наберуть такого вигляду:
 (209)
(209)
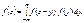 (210)
(210)
Формули (209), (210) називають згорткою, або композицією, двох законів. 4.3. Знаходження F(Z), f (z), якщо Z = ХY.
Якщо Z =ХY, тобто випадкова величина Z дорівнює добутку двох випадкових величин Х і Y, то ймовірність потрапляння випадкової величини Z в область 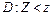
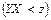 унаочнює рис. 83.
унаочнює рис. 83.
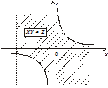
Рис. 83
Маємо:
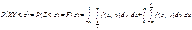
або 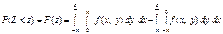 . (215)
. (215)
Скориставшись (215), дістанемо
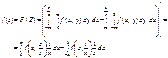
Отже, 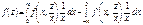 (216)
(216)
Якщо випадкові величини Х і Y є незалежними, то
 .
.
4.2. Знаходження F (z), f (z), якщо 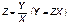
Оскільки пряма Y = ZХ ділить площину хОу на дві непересічені області, зображені на рис. 82.
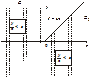
Рис. 82
В області D1 виконується випадкова подія 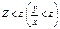 і в області
і в області 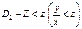 . Отже, імовірність події
. Отже, імовірність події  дорівнюватиме сумі ймовірностей двох несумісних випадкових подій, що зможуть відбутися або в області
дорівнюватиме сумі ймовірностей двох несумісних випадкових подій, що зможуть відбутися або в області  , або в області
, або в області 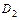 :
:
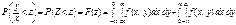 .
.
Отже,
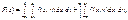 (211)
(211)
або
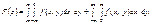 (212)
(212)
Щільність імовірностей

Остаточно маємо:
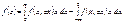 (213)
(213)
Якщо Х і Y є незалежними, то
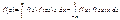 . (214)
. (214)
Дата добавления: 2014-11-29; просмотров: 1323;
