Локальная теорема Лапласа.

Вероятность того, что в n, независимых испытаниях, в каждом из которых вероятность появления события равна p (0<p<1), событие наступит ровно k раз (безразлично в какой последовательности), выражается приближенным равенством

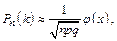
где 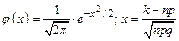. Функция 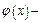четная, т.е. .

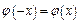При x>5 можно считать, что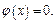

Интегральная теорема Лапласа.

Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна p (0<p<1), событие наступит не менее k₁ раз и не более k₂ раз выражается приближенным равенством

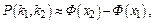
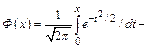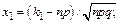
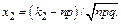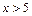где функцияЛапласа; При полагают Ф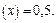

Функция Лапласа четная, т.е. Ф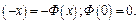

4. Нормальнымраспределением называют распределение вероятностей непрерывной случайной величины X, плотность распределения которого имеет вид

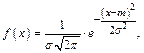
где m–математическое ожидание, а 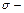среднее квадратическое отклонение величины X.

Вероятность того, что x примет значение, принадлежащее интервалу 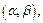составляет

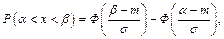(4)

где Ф 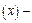функция Лапласа.

Вероятность того, что абсолютная величина отклонения меньше положительного числа 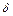, выражается равенством

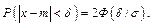(5)

Пример 1. Собрание, на котором присутствуют 25 человек, в том числе 5 женщин, выбирают делегацию из 5 человек. Считая, что каждый из присутствующих с одинаковой вероятностью может быть избран, найти вероятность того, что в делегацию войдут 2 женщины и 3 мужчины.

Решение. Число всех способов выбора 5 человек из 25 равно 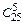, а число способов выбора двух женщин из 5 равно 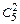. Каждая такая двойка может сочетаться с каждой тройкой из 20 мужчин. Число таких троек равно 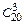. Искомая вероятность составляет

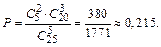
Пример 2. Слово 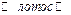, составленное из букв-кубиков, рассыпано на отдельные буквы, которые затем сложены в коробке. Из коробки наугад извлекают одну за другой три буквы. Какова вероятность того, что при этом появится слово ?

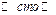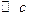
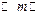Решение. Вероятность появления буквы равна 1/5. Вероятность появления вслед за ней буквы равна 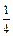, и, наконец, вероятность появления буквы 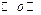равна 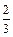. Искомая вероятность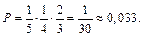

Пример 3. Случайно встреченное лицо с вероятностью 0,2 может оказаться брюнетом, с вероятностью 0,3 – блондином, с вероятностью 0,4 – шатеном и с вероятностью 0,1 – рыжим. Каковая вероятность того, что среди пяти случайно встреченных лиц: а) не менее четырех блондинов; б) два блондина и три шатена; в) хотя бы один рыжий?

Решение. а) Искомая вероятность составляет (см. формулу (1))

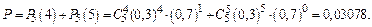
б) Искомая вероятность

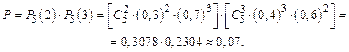
в) Искомая вероятность

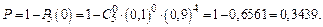
Пример 4. Игральную кость подбрасывают 500 раз. Какова вероятность того, что шестерка при этом выпадет 50 раз?

Решение. Здесь 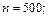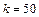; p=1/6; q=5/6; 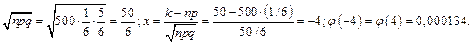По формуле (2) находим искомую вероятность:

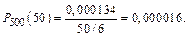
Пример 5. Пусть вероятность того, что покупателю необходимо купить обувь 41-го размера, равна 0,2. Найти вероятность того, что из 400 покупателей не более 100 потребуют обувь этого размера.

Решение. По условию, n=400; p=0,2; q=0,8;

;

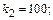
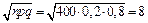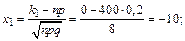
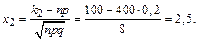Согласно формуле (3), искомая вероятность есть

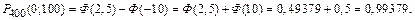
Пример 6. Непрерывная случайная величина X распределена нормально. Известно, что D(x)=4 и P( 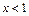)=0,5. Найти Р(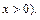

Решение. По формуле (4) получим

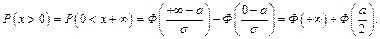
Найдем а. Имеем

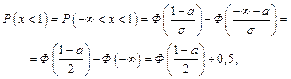
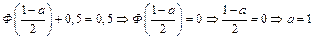
Окончательно находим

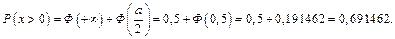
Пример 7. Среднее квадратическое отклонение случайной величины, распределенной по нормальному закону, равно 2; М(x)=16. Найти границы, в которых с вероятностью 0,95 следует ожидать значения случайной величины.

Решение. По формуле (5) имеем

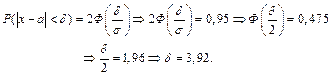
Найдем границы интервала:

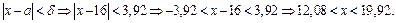
Список литературы

1. Баранова Е.С., Васильева Н.В., Федотов В.П. Практическое пособие по высшей математике. Типовые расчеты: Учебное пособие.-СПб.:Питер, 2008.-320 с.:ил.

2. Данко П.Е.,Попов А.Г.,Кожевникова Т.Я. Высшая математика в упражнениях и задачах. В 2 ч. Ч.1: Учебное пособие для вузов.-М.:ООО «Издательский дом «ОНИКС 21 век»: ООО «Издательство «Мир и Образование», 2003.-304 с.:ил.

3. Данко П.Е.,Попов А.Г.,Кожевникова Т.Я. Высшая математика в упражнениях и задачах. В 2 ч. Ч.2: Учебное пособие для вузов.-М.:ООО «Издательский дом «ОНИКС 21 век»: ООО «Издательство «Мир и Образование», 2003.-416 с.:ил.

4. Меняйлов А.И. математический практикум: Учебное пособие для высшей школы.-М.: Академический Проект, 2003.-192 с.

5. Мироненко Е.С. Высшая математика: Методические указания и контрольные задания для студентов- заочников.-2-е изд., стер.-М.: Высш. шк., 2000.-110 с.:ил.