Решение. Пример 3. Вычислить приближенно исходя из значения функции

Следовательно, 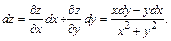
Пример 3. Вычислить приближенно  исходя из значения функции
исходя из значения функции 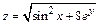 при
при 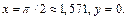
Решение. Искомое число есть наращенное значение функции z при  Найдем значение z при
Найдем значение z при 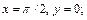 имеем
имеем 
Находим приращение функции:

Следовательно, 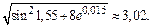
Пример 4. Вычислить приближенно 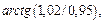 исходя из значения функции
исходя из значения функции  при
при 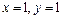 .
.
Решение. Значение функции z при x=1, y=1 есть 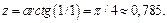
Найдем приращение функции 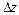 при
при 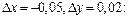
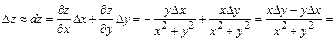
= 
Следовательно, 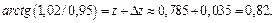
Пример 5. 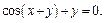 Найти
Найти 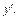
Решение. Здесь 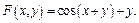
Найдем 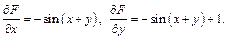
Следовательно,

Пример 6. 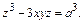 Найти
Найти 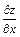 и
и 
Решение. Здесь 
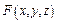 =
= 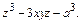
Находим 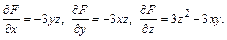
Тогда 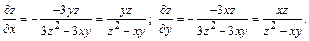
Пример 7. Найти экстремум функции 
Решение. Находим частные производные первого порядка: 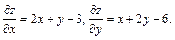 Воспользовавшись необходимыми условиями экстремума, находим стационарные точки:
Воспользовавшись необходимыми условиями экстремума, находим стационарные точки:
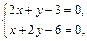 откуда
откуда 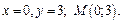
Находим значения частных производных второго порядка в точке M:
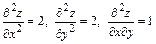
и составляем дискриминант 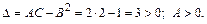 Следовательно, в точке
Следовательно, в точке 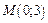 заданная функция имеет минимум. Значение функции в этой точке
заданная функция имеет минимум. Значение функции в этой точке 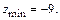
Пример 6. Найти экстремум функции
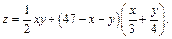
Решение. Находим частные производные первого порядка:
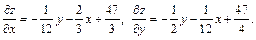
Воспользовавшись необходимыми условиями экстремума, находим стационарные точки:

Отсюда x=21, y=20; стационарная точка 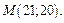
Найдем значения вторых производных в точке M: 
Тогда 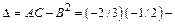
 .
.
Так как A<0, то в точке 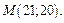 функция имеет максимум:
функция имеет максимум: 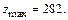
Дата добавления: 2014-12-03; просмотров: 1176;
