Тема 11. Элементы теории вероятностей.

Основные теоретические сведения.

1. При классическом определении вероятность события А определяется соотношением где m–число элементарных исходов испытания, благоприятствующих наступления события А, а n–общее число возможных элементарных исходов испытания. Предполагается, что элементарные исходы единственно возможны и равновозможны. Относительная частота события А есть , где m–число испытаний, в которых событие А наступило, а n–общее число произведенных испытаний.

При статистическом определении в качестве вероятности события принимают его относительную частоту.

2. Схема испытаний Бернулли (повторение опытов). Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна p (0<p<1), событие наступит ровно k раз (безразлично в какой последовательности), есть

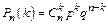,где q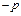=1 , . (1)

Вероятность того, что событие наступит:

а) менее k раз: P_n(0)+P_n(1)+ … +P_n(k 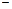1),

б) более k раз: P_n(k+1)+P_n(k+2)+ … +P_n(n),

в) не менее k раз: P_n(k)+P_n(k+1)+ … +P_n(n),

г) не более k раз: P_n(0)+P_n(1)+ … +P_n(k).

3.Если число испытаний n велико, то применение формулы Бернулли приводит к громоздким вычислениям. В таких случаях пользуются предельными теоремами Лапласа.