Частные производные и дифференциалы высших порядков.
Частными производными второго порядка от функции 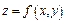 называются частные производные от ее частных производных первого порядка .
называются частные производные от ее частных производных первого порядка .
Обозначение частных производных второго порядка:
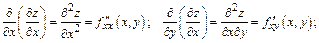
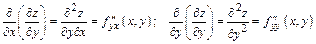 .
.
Аналогично определяются и обозначаются частные производные третьих и высших порядков, например:
 и т.д.
и т.д.
Так называемые «смешанные» производные, отличающиеся друг от друга лишь последовательностью дифференцирования, равны между собой, если они непрерывны, например:
 .
.
Дифференциалом второго порядка от функции 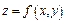 называется дифференциал от ее полного дифференциала, т.е.
называется дифференциал от ее полного дифференциала, т.е. 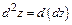 .
.
Аналогично определяются дифференциалы третьего и высших порядков:  ; вообще
; вообще 
Если x и y – независимые переменные и функция 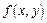 имеет непрерывные частные производные, то дифференциалы высших порядков вычисляются по формулам:
имеет непрерывные частные производные, то дифференциалы высших порядков вычисляются по формулам:
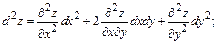
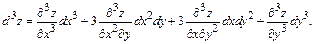
Дата добавления: 2014-12-03; просмотров: 1240;
