Дифференцирование неявных функций.
Производная неявной функции  , заданной с помощью уравнения
, заданной с помощью уравнения  , где
, где 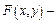 дифференцируемая функция переменных
дифференцируемая функция переменных 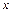 и
и 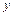 , может быть вычислена по формуле
, может быть вычислена по формуле
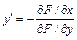 при условии
при условии 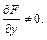
Производные высших порядков неявной функции можно найти последовательным дифференцированием указанной формулы, рассматривая при этом 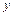 как функцию от
как функцию от 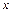 .
.
Аналогично, частные производные неявной функции двух переменных  , заданной с помощью уравнения
, заданной с помощью уравнения  , где
, где 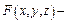 дифференцируемая функция переменных
дифференцируемая функция переменных 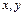 и
и 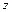 , могут быть вычислены по формулам
, могут быть вычислены по формулам
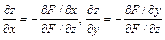 при условии
при условии 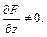
6. Экстремум функции.
Функция 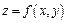 имеет максимум (минимум) в точке
имеет максимум (минимум) в точке  , если значение функции в этой точке больше (меньше), чем ее значение в любой другой точке
, если значение функции в этой точке больше (меньше), чем ее значение в любой другой точке  некоторой окрестности точки
некоторой окрестности точки  , т.е.
, т.е. 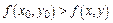 [соответственно
[соответственно  ] для всех точек
] для всех точек 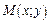 , удовлетворяющих условию
, удовлетворяющих условию 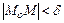 , где
, где 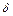
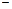 достаточно малое положительное число.
достаточно малое положительное число.
Максимум или минимум функции называется ее экстремумом. Точка  , в которой функция имеет экстремум, называется точкой экстремума.
, в которой функция имеет экстремум, называется точкой экстремума.
Если дифференцируемая функция 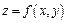 достигает экстремума в точке
достигает экстремума в точке  , то ее частные производные первого порядка в этой точке равны нулю, т.е.
, то ее частные производные первого порядка в этой точке равны нулю, т.е.
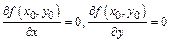
(необходимые условия экстремума).
Точки, в которых частные производные равны нулю, называются стационарными точками. Не всякая стационарная точка является точкой экстремума.
Пусть 
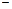 стационарная точка функции
стационарная точка функции 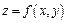 . Обозначим
. Обозначим
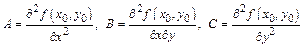
и составим дискриминант 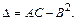 Тогда:
Тогда:
а) если 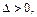 то функция имеет в точке
то функция имеет в точке  экстремум, а именно максимум при
экстремум, а именно максимум при  и минимум при
и минимум при 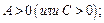
б) если 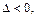 то в точке
то в точке  экстремума нет (достаточные условия наличия или отсутствия экстремума);
экстремума нет (достаточные условия наличия или отсутствия экстремума);
в) если  то требуется дальнейшее исследование (сомнительный случай).
то требуется дальнейшее исследование (сомнительный случай).
Пример 1.Дана функция 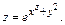 Найти
Найти 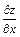 и
и  .
.
Дата добавления: 2014-12-03; просмотров: 1532;
