Повторные испытания. Формула Бернулли
Пусть производится n независимых испытаний, в каждом из которых событие А может появиться или не появиться. Будем считать, что вероятность появления события А в каждом испытании постоянна и равна р. Тогда вероятность появления события А в каждом испытании будет также величиной постоянной и равна
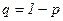 .
.
Найдем вероятность того, что в n независимых испытаниях событие А появится k раз и соответственно не появится n-k раз.
По теореме умножения вероятностей независимых событий вероятность одного сложного события, состоящего в том, что в n независимых испытаниях событие А появится k раз и не появится n-k раз равна: 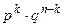 . А таких сложных событий будет столько, сколько можно составить сочетаний из n элементов по k, то есть
. А таких сложных событий будет столько, сколько можно составить сочетаний из n элементов по k, то есть 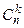 . Так как эти сложные события не совместны, то по теореме сложения вероятностей несовместных событий искомая вероятность равна вероятности одного сложного события, умноженный на их число, то есть:
. Так как эти сложные события не совместны, то по теореме сложения вероятностей несовместных событий искомая вероятность равна вероятности одного сложного события, умноженный на их число, то есть:

Эту формулу называют формулой Бернулли.
Заметим, что формула Бернулли применяется тогда, когда число испытаний не велико  и вероятность появления события А в каждом испытании отлична от 0 и 1.
и вероятность появления события А в каждом испытании отлична от 0 и 1.
Пример.Вероятность того, что расход электроэнергии на протяжении одних суток не превысит установленной нормы, равна 0,75. Найти вероятность того, что в ближайшие 8 суток расход электроэнергии в течении 4 суток не превысит нормы.
Решение.Вероятность нормального расхода электроэнергии на протяжении каждых из 8 суток постоянна и равна: р=0,75. Тогда вероятность перерасхода электроэнергии в каждые сутки также постоянна и равна: 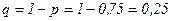
Число испытаний невелико, поэтому искомая вероятность находится по формуле Бернулли:
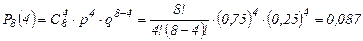
Дата добавления: 2014-12-05; просмотров: 1561;
