Формула полной вероятности. Формула Бейеса.
Пусть требуется определить вероятность некоторого события А, которое может произойти вместе с одним из событий h1,h2,...,hn, образующих полную группу несовместных событий. Будем эти события называтьгипотезами.
В этом случае вероятность события А вычисляется как сумма произведений вероятности каждой гипотезы на условную вероятность события при этой гипотезе:
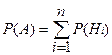 Р(А|Нi).
Р(А|Нi).
Последнюю формулу называютформулой полной вероятности.
Пример. Имеются три одинаковых на вид урны; в первой урне 2 белых и 1 черный шар; во второй - 3 белых и 1 черный; в третьей - 2 белых и 2 черных шара. Некто выбирает наудачу одну из урн и вынимает из нее шар. Найти вероятность того, что этот шар - белый.
Решение. Рассмотрим 3 гипотезы:
Н1 - выбор первой урны;
H2 - выбор второй урны;
H3 - выбор третьей урны;
и событие А - появление белого шара.
Так как гипотезы, по условию задачи, равновозможны, то Р(Н1)=Р(Н2)=Р(Н3)= 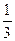 .
.
Условные вероятности события А при этих гипотезах соответственно равны р(а|н1)= 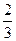 ; Р(А|Н2)=
; Р(А|Н2)= 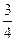 ; Р(А|Н3)=
; Р(А|Н3)= 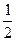 .
.
По формуле полной вероятности  .
.
Следствием теоремы умножения и формулы полной вероятности является формула Бейеса.
 для
для 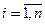 .
.
Пример. На предприятии изготавливаются изделия определенного вида на трех поточных линиях. На первой линии производится 20% изделий от всего объема их производства, на второй - 30%, на третьей, - 50%. Каждая из линий характеризуется соответственно следующими процентами брака: 5%, 2%, 3%. Наугад взятое изделие оказалось бракованным, требуется определить вероятность того, что оно сделано на первой линии.
Решение. Обозначим Н1, H2, H3 события, состоящие в том, что наугад взятое изделие произведено на первой, второй и третьей линиях.
Согласно условиям задачи Р(Н1)=0,2; Р(Н2)=0,3; Р(Н3)=0,5.
Обозначим А - событие, состоящее в том, что наугад взятое изделие оказалось бракованным.
По условиям задачи Р(А|Н1)=0,05; Р(А|Н2)=0,02; Р(А|Н3)=0,03.
По формуле Бейеса имеем
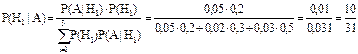 .
.
Дата добавления: 2014-12-05; просмотров: 3812;
