Дифференциальные уравнения первого порядка с разделяющимися переменными
Дифференциальные уравнения вида:
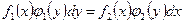 (1)
(1)
называются уравнениями с разделяющимися переменными. Решая такие уравнения, необходимо преобразовать их так, чтобы одна часть уравнения содержала только переменную у, а другая - только х, а затем проинтегрировать обе части (по у и по х соответственно).
Например, уравнение (1) надо разделить на  , тогда получим
, тогда получим 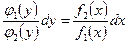 . Проинтегрировав обе части, найдем общий интеграл:
. Проинтегрировав обе части, найдем общий интеграл:
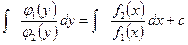 . (2)
. (2)
Кроме найденного общего интеграла (2) уравнению (1) могут также удовлетворять решения, получаемые из уравнения  . Если эти решения не входят в общий интеграл (2), то они будут особыми решениями уравнения (1).
. Если эти решения не входят в общий интеграл (2), то они будут особыми решениями уравнения (1).
Пример.Скорость размножения некоторых бактерий пропорционально количеству бактерий, имеющихся в наличии в рассматриваемый момент времени. Известно, что количество бактерий за один час утроилось. Как изменится количество бактерий через 5 часов, если первоначальное количество равно a.
Решение. Пусть х — количество бактерий в момент времени t. Переменная величина х является функцией переменной величины t. Скорость изменения величины х выражается производной 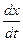 . По условию задачи дифференциальное уравнение, описывающее рассматриваемый процесс, имеет вид
. По условию задачи дифференциальное уравнение, описывающее рассматриваемый процесс, имеет вид 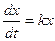 , где k — некоторый коэффициент пропорциональности. Разделим переменные и решим составленное уравнение:
, где k — некоторый коэффициент пропорциональности. Разделим переменные и решим составленное уравнение:

откуда  , или
, или 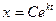 — общее решение уравнения.
— общее решение уравнения.
Значение произвольной постоянной С определяем из начальных условий: при t = 0, х = а. Следовательно, 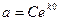 ; C = a. Таким образом,
; C = a. Таким образом, 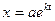 , или
, или  — есть частное решение, удовлетворяющее заданным начальным условиям.
— есть частное решение, удовлетворяющее заданным начальным условиям.
Чтобы определить коэффициент пропорциональности k, воспользуемся теми дополнительными условиями, которые указаны в задаче: при t=1 (за один час) количество бактерий устроилось, т. е. x=3a. Следовательно, 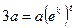 , откуда
, откуда 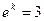 , и мы получаем зависимость между переменными:
, и мы получаем зависимость между переменными: 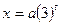 .
.
Чтобы ответить на вопрос задачи, находим количество х при t=5: 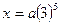 ,
,  . Как видно, через 5 ч количество бактерий увеличится в 243 раза.
. Как видно, через 5 ч количество бактерий увеличится в 243 раза.
Пример. Найти общий интеграл дифференциального уравнения (ответ представить в виде y(х, у)=с).
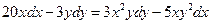 .
.
Решение. Уравнение представлено в дифференциальной форме. Для разделения переменных перенесем все слагаемые в одну часть уравнения и сгруппируем содержащие dx и dy:
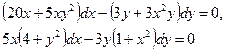
Разделим обе части уравнения на 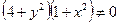 , получим
, получим
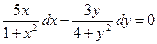 .
.
Почленно интегрируя, получим искомый общий интеграл:
 .
.
В первообразных модули можно опустить, т.к. 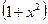 и
и 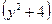 величины всегда неотрицательные.
величины всегда неотрицательные.
Умножая обе части уравнения на 2 и учитывая свойства логарифма, получим
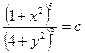 .
.
Дата добавления: 2014-12-05; просмотров: 2114;
