ИДЗ-7. Исследование функции на непрерывность

Исследовать данную функцию на непрерывность и построить ее график:

Решение: Функция f(x) определена и непрерывна на трех интервалах (–¥; 0), (0; 2) и (2; +¥), где она задана непрерывными элементарными функциями. Следовательно, разрыв функции возможен лишь в точках x₁ = 0 и x₂ = 2. Исследуем f(x) на непрерывность в них.

Точка x₁ = 0. Для этой точки f(x₁ = 0) = 0² = 0. Предел слева: A₁ = 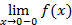= 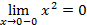. Предел справа: A₂ = 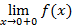= 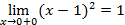¹ A₁. Таким образом, функция f(x) в точке x₁ = 0 имеет (неустранимый) разрыв I рода. Точка x₂ = 2. Для этой точки f(x₂ = 2) = (x – 1)² = 1. Предел слева: A₁ = 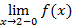= 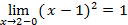. Предел справа: A₂ = 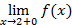= 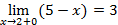¹ A₁. Таким образом, функция f(x) в точке x₂ = 2 также имеет (неустранимый) разрыв I рода. График f(x) дан на рис. 1.

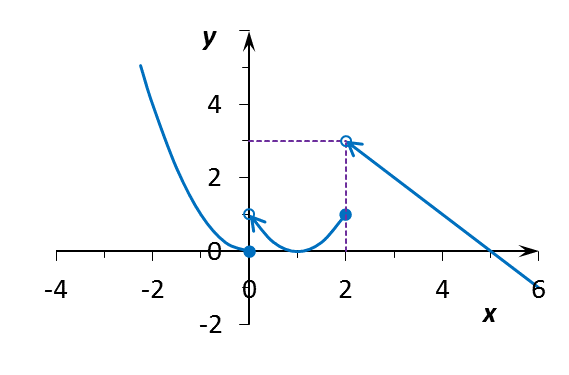
Рис. 1.

Ответ: Функция f(x) (рис. 1) претерпевает разрывы I рода в точках x₁ = 0 и x₂ = 2.