ИДЗ-4. Решение однородной системы линейных алгебраических уравнений

Решить однородную систему линейных алгебраических уравнений:

а) 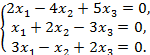б)

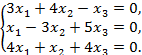
Решение: а) Вычислим определитель системы:

D = = = 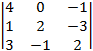= 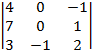–(–1)× 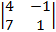= 4 + 7 = 11 ¹ 0.

Т.к. определитель D однородной системы линейных уравнений отличен от нуля, то система имеет единственное нулевое (тривиальное) решение x₁ = x₂ = x₃ = 0.

б) Вычислим определитель системы:

D = = = = 0.

Т.к. определитель D однородной системы линейных уравнений равен нулю, то система имеет бесчисленное множество решений. Нетрудно убедиться, что ранг матрицы данной системы уравнений размерности n = 3 равен r_A = 2. Иными словами, в данной системе уравнений независимыми являются только два уравнения из трех; используем, например, первое и второе уравнения:

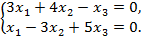
Так как определитель D₂ = = –9 – 4 = –13 из коэффициентов при неизвестных x₁ и x₂ не равен нулю, то в качестве базисных неизвестных можно взять x₁ и x₂. С учетом сказанного, систему можно переписать в виде:

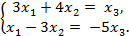
Решение этой системы получим с помощью формул Крамера:

x₁ = 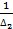× 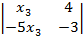= = 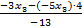– 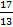x₃;

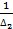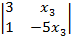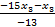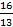x₂ = × = = x₃.

Таким образом, нетривиальным решением системы является тройка действительных чисел x₁ = – 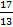x₃, x₂ = 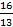x₃, x₃ Î R.

Ответ: а) x₁ = x₂ = x₃ = 0; б) x₁ = – 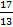x₃, x₂ = 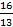x₃, x₃ Î R.