ИДЗ-1. Действия с определителями

Для данного определителя D:

D = .

а) найти алгебраические дополнения элементов 1-ой строки и 1-го столбца; б) вычислить определитель D, приведя его к треугольному виду, или получив предварительно нули в к.-л. строке или столбце; в) проверить расчет, применяя разложение определителя по элементам 1-ой строки или 1-го столбца и используя алгебраические дополнения соответствующих элементов из задания а).

Решение: а) Как известно, алгебраическим дополнением A_ij элемента a_ij данного определителя D называется определитель порядка на единицу меньшего, полученный из исходного путем вычеркивания i-ой строки и j-ого столбца; при этом знак алгебраического дополнения определяется как (–1)^i+j. В данной задаче,

A₁₁ = (–1)¹⁺¹× = = = – = –(–2×8 – (–1)×6) = 10;

A₁₂ = (–1)¹⁺²× = – = – = = 6×8 – 5×6 = 18;

A₁₃ = (–1)¹⁺³× = = = – = –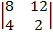(8×2 – 4×12) = 32;

A₁₄ = (–1)¹⁺⁴× 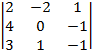= – = – 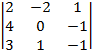= – = 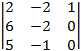= 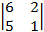6 – 10 = –4;

A₂₁ = (–1)²⁺¹× 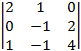= – = – 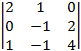= = 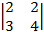2×4 – 3×2 = 2;

A₃₁ = (–1)³⁺¹× 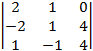= = 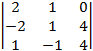= = 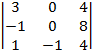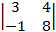3×8 + 1×4 = 28;

A₄₁ = (–1)⁴⁺¹× = – = – = –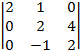2× = –2×(2×2 + 1×4) = –16.

б) Вычислить определитель D, приведя его к треугольному виду, или получив предварительно нули в к.-л. строке или столбце:

D = = = 1× = =

= = (–1)× = 2× 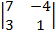= 2×(7×1 + 3×4) = 38.

в) проверим расчет, применяя разложение определителя по элементам 1-ой строки и (или) 1-го столбца и используя алгебраические дополнения соответствующих элементов из задания а).

Разложение по первой строке:

D = a₁₁A₁₁ + a₁₂A₁₂ + a₁₃A₁₃ + a₁₄A₁₄ = (–3)×10 + 2×18 + 1×32 + 0×(–4) = –30 + 36 + 32 = 38.

Разложение по первому столбцу:

D = a₁₁A₁₁ + a₂₁A₂₁ + a₃₁A₃₁ + a₄₁A₄₁ = (–3)×10 + 2×2 + 4×28 + 3×(–16) = –30 + 4 + 112 – 48 = 38.

Ответ: а) Алгебраические дополнения: A₁₁ = 10; A₁₂ = 18; A₁₃ = 28; A₁₄ = –4; A₂₁ = 2; A₃₁ = 28; A₄₁ = –16; б), в) величина определителя D = 38.