ИДЗ-3. Решение неоднородной системы линейных алгебраических уравнений
Проверить совместность системы уравнений и в случае совместности решить ее: а) по правилам Крамера; б) с помощью обратной матрицы (матричным методом); в) методом Гаусса:
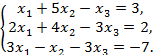
Решение: Совместность данной системы линейных неоднородных алгебраических уравнений проверим по теореме Кронекера – Капелли, утверждающей, что система совместна тогда и только тогда, когда ранги основной (rA) и расширенной (rB) матриц системы равны: rA = rB = r. При этом, если r = n, где n – порядок системы, система имеет единственное решение.
Рангом матрицы называется наиболее высокий порядок определителя, составленного из ее элементов, отличный от нуля.
В данном случае, определитель основной матрицы A системы уравнений:
D = 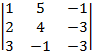 =
= 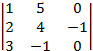 = –(–1)×
= –(–1)× 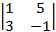 = 1×(–1) – 3×5 = –16 ¹ 0,
= 1×(–1) – 3×5 = –16 ¹ 0,
т.е. rA = 3 = n. Установим значения определителей, составленных из элементов расширенной матрицы, заменяя последовательно столбцом свободных членов 1-ый, 2-ой и 3-ий столбцы основной матрицы системы:
detB1 = 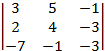 =
=  =
= 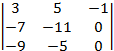 = (–1)×
= (–1)× 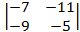 =
=
= –(35–99) = 64 ¹ 0;
detB2 = 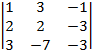 =
= 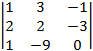 =
= 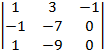 = (–1)×
= (–1)× 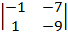 = –(9 + 7) =
= –(9 + 7) =
= –16 ¹ 0;
detB3 = 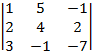 =
=  =
= 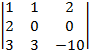 = (–2)×
= (–2)× 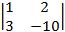 = –2×(–10 – 6) =
= –2×(–10 – 6) =
= 32 ¹ 0.
т.е. rB = 3 = rA. Т.о., ранги основной и расширенной матриц системы совпадают и равны числу переменных n = 3, т.е. система однозначно разрешима.
а) Для нахождения решения системы применим правила Крамера, используя значения вычисленных выше определителей:
x1 =  ×detB1 = –
×detB1 = – 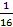 ×64 = –4;
×64 = –4;
x2 =  ×detB2 = –
×detB2 = – 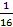 ×(–16) = 1;
×(–16) = 1;
x3 =  ×detB3 = –
×detB3 = –  ×32 = –2.
×32 = –2.
Окончательно, решение системы есть 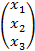 =
= 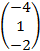 .
.
б) Для нахождения решения системы с помощью обратной матрицы запишем систему уравнений в матричной форме:
A× 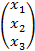 =
= 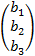 ,
,
где A = 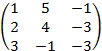 – матрица системы;
– матрица системы; 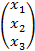 и
и 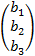 =
= 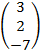 – столбец переменных и свободных членов, соответственно. Тогда решение системы в матричном виде есть:
– столбец переменных и свободных членов, соответственно. Тогда решение системы в матричном виде есть:
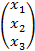 = A–1×
= A–1× 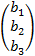 .
.
Остается найти обратную матрицу A–1 системы. Для этого вычислим матрицу дополнений и транспонируем ее, т.е. вычислим присоединенную матрицу A* к матрице A.
A11 = (–1)1+1× 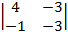 = 4×(–3) – 1×3 = –15;
= 4×(–3) – 1×3 = –15;
A12 = (–1)1+2×  = –(2×(–3) + 3×3) = –3;
= –(2×(–3) + 3×3) = –3;
A13 = (–1)1+3× 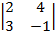 = 2×(–1) – 3×4 = –14;
= 2×(–1) – 3×4 = –14;
A21 = (–1)2+1× 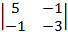 = –(5×(–3) – 1×1) = 16;
= –(5×(–3) – 1×1) = 16;
A22 = (–1)2+2× 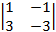 = –(1×(–3) – 3×(–1)) = 0;
= –(1×(–3) – 3×(–1)) = 0;
A23 = (–1)2+3× 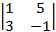 = –(1×(–1) – 3×5) = 16;
= –(1×(–1) – 3×5) = 16;
A31 = (–1)3+1× 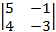 = 5×(–3) – 4×(–1) = –11;
= 5×(–3) – 4×(–1) = –11;
A32 = (–1)3+2× 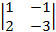 = –(1×(–3) – 2×(–1)) = 1;
= –(1×(–3) – 2×(–1)) = 1;
A33 = (–1)3+3× 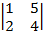 = 1×4 – 2×5 = –6.
= 1×4 – 2×5 = –6.
Теперь присоединенной матрицей будет матрица A* =  , а обратной матрицей – матрица A–1 =
, а обратной матрицей – матрица A–1 = 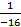 ×
×  .
.
Решением системы будет
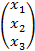 = A–1×
= A–1× 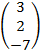 =
= 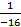 ×
×  ×
× 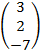 = –
= – 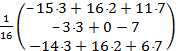 × =
× =
= – 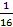 ×
× 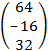 =
= 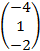 .
.
в) Решим данную систему методом Гаусса (методом исключения):
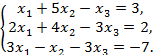
Исключим x1 из второго и третьего уравнений. Для этого первое уравнение умножим на 2 и вычтем из второго уравнения; первое уравнение умножим на 3 и вычтем из третьего уравнения. Получим
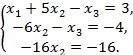
Последовательно находим x2 = 1; x3 = 4 – 6×1 = –2; x1 = 3 – 5×1 –2 = –4.
Ответ: Решение системы: 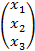 =
= 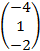 .
.
Дата добавления: 2014-12-06; просмотров: 2294;
